题目内容
函数y=-cos2x+cosx(x∈R)的值域是 .
考点:函数的值域
专题:函数的性质及应用,三角函数的求值
分析:令t=cosx,t∈[-1,1],利用二次函数的图象和性质即可得到结论.
解答:
解:令t=cosx,t∈[-1,1],
则y=-cos2x+cosx=-t2+t,t∈[-1,1],
∵y=-t2+t的图象是开口朝下,且以直线x=
为对称轴的抛物线,
故当t=-1时,y取最小值-1,当t=
时,y取最大值
,
故函数y=-cos2x+cosx(x∈R)的值域是[-2,
],
故答案为:[-2,
]
则y=-cos2x+cosx=-t2+t,t∈[-1,1],
∵y=-t2+t的图象是开口朝下,且以直线x=
| 1 |
| 2 |
故当t=-1时,y取最小值-1,当t=
| 1 |
| 2 |
| 1 |
| 4 |
故函数y=-cos2x+cosx(x∈R)的值域是[-2,
| 1 |
| 4 |
故答案为:[-2,
| 1 |
| 4 |
点评:本题主要考查函数的值域的计算,利用二次函数的图象和性质是解决本题的关键,难度不大,属于基础题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
命题“x2-9=0的解是x=±3”,在这个命题中,使用的逻辑联结词的情况是( )
| A、没有使用逻辑联结词 |
| B、使用了“且” |
| C、使用了“或” |
| D、使用了“非” |
用数学归纳法证明等式(n+1)(n+2)×…×(n+n)=2n×1×3×…×(2n-1)的过程中,由n=k(k∈N*)推出n=k+1(k∈N*)成立时,左边应增加的因式是( )
| A、2k+1 | ||
| B、2(2k+1) | ||
C、
| ||
D、
|
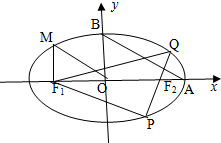 如图,从椭圆
如图,从椭圆