题目内容
已知
，
是夹角为120°的单位向量，向量
=t
+（1-t）
，若
⊥
，则实数t= ．
| m |
| n |
| a |
| m |
| n |
| n |
| a |
考点：数量积判断两个平面向量的垂直关系
专题：平面向量及应用
分析：由已知得
•
=
[t
+（1-t）
]=0，由此能求出实数t．
| n |
| a |
| n |
| m |
| n |
解答：
解：∵
，
是夹角为120°的单位向量，
向量
=t
+（1-t）
，
⊥
，
∴
•
=
[t
+（1-t）
]
=t
•
+（1-t）
2
=t•cos120°+1-t=1-
t=0，
解得t=
．
故答案为：
．
| m |
| n |
向量
| a |
| m |
| n |
| n |
| a |
∴
| n |
| a |
| n |
| m |
| n |
=t
| n |
| m |
| n |
=t•cos120°+1-t=1-
| 3 |
| 2 |
解得t=
| 2 |
| 3 |
故答案为：
| 2 |
| 3 |
点评：本题考查实数值的求法，是基础题，解题时要认真审题，注意向量垂直的性质的合理运用．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
当λ变化时，直线λx-y+2+λ=0经过的定点是（ ）
| A、（1，2） |
| B、（-1，2） |
| C、（1，-2） |
| D、（-1，-2） |
如图，在正方体ABCD-A1B1C1D1中，E为AB中点，设I为全集，集合M，N，P都是其子集，则图中的阴影部分表示的集合为（ ）
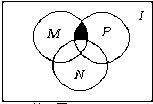
| A、M∩（N∪P） |
| B、M∩（P∩∁IN） |
| C、P∩（∁IN∩∁IM ） |
| D、（M∩N）∪（M∩P） |
在等比数列{an}中，a1=
，a4=
，则数列的公比q为（ ）
| 1 |
| 2 |
| 1 |
| 16 |
A、
| ||
B、±
| ||
C、
| ||
D、±
|