题目内容
17.若函数y=loga(x2-ax+$\frac{1}{2}$)有最小值,则a的取值范围是( )| A. | 0<a<1 | B. | 0<a<$\sqrt{2}$,a≠1 | C. | 1<a<$\sqrt{2}$ | D. | a≥$\sqrt{2}$ |
分析 由题意和二次函数以及复合函数可得a>1且$\frac{2-{a}^{2}}{4}$>0,解不等式组可得.
解答 解:由题意可得二次函数t=x2-ax+$\frac{1}{2}$有最小值$\frac{4×1×\frac{1}{2}-{a}^{2}}{4×1}$=$\frac{2-{a}^{2}}{4}$,
要使函数y=loga(x2-ax+$\frac{1}{2}$)有最小值,需a>1且$\frac{2-{a}^{2}}{4}$>0,
解得1<a<$\sqrt{2}$,
故选:C.
点评 本题考查对数函数的性质,涉及转化思想和二次函数的最值,属基础题.

练习册系列答案
相关题目
5.设a=($\frac{7}{9}$)${\;}^{-\frac{1}{4}}$,b=($\frac{9}{7}$)${\;}^{\frac{1}{5}}$,c=log2$\frac{7}{9}$,则a,b,c的大小顺序是( )
| A. | b<a<c | B. | c<b<a | C. | c<a<b | D. | b<c<a |
12.“a=-3”是“函数y=x2+2(a-1)x+2在区间(-∞,4]上单调递减”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
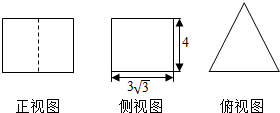 若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如图所示,则这个棱柱的表面积为$72+18\sqrt{3}$.则这个棱柱体积为36$\sqrt{3}$.
若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如图所示,则这个棱柱的表面积为$72+18\sqrt{3}$.则这个棱柱体积为36$\sqrt{3}$.