题目内容
5.三个数a,b,c成等比数列,且a+b+c=3,则b的取值范围是[-3,0)∪(0,1].分析 三个数a,b,c成等比数列,且a+b+c=3,可得b2=ac≤$(\frac{a+c}{2})^{2}$=$(\frac{3-b}{2})^{2}$,b≠0.解出即可得出.
解答 解:∵三个数a,b,c成等比数列,且a+b+c=3,
∴b2=ac≤$(\frac{a+c}{2})^{2}$=$(\frac{3-b}{2})^{2}$,b≠0.
化为:b2+2b-3≤0,
解得-3≤b≤1,且b≠0.
则b的取值范围是[-3,0)∪(0,1];
故答案为:[-3,0)∪(0,1].
点评 本题考查了等比数列的性质、重要不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
18.已知4sinα+3cosα=0,则tanα的值是( )
| A. | $\frac{3}{4}$ | B. | $-\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | $-\frac{4}{3}$ |
17.若函数y=loga(x2-ax+$\frac{1}{2}$)有最小值,则a的取值范围是( )
| A. | 0<a<1 | B. | 0<a<$\sqrt{2}$,a≠1 | C. | 1<a<$\sqrt{2}$ | D. | a≥$\sqrt{2}$ |
20.给出下列四个命题:
①若平面α∥β,直线a?α,直线b?β,则a∥b
②若直线a∥b,a∥α,则b∥α
③若平面α∥β,直线a?α,则a∥β
④若直线a∥α,a∥β,则α∥β
其中正确命题有( )
①若平面α∥β,直线a?α,直线b?β,则a∥b
②若直线a∥b,a∥α,则b∥α
③若平面α∥β,直线a?α,则a∥β
④若直线a∥α,a∥β,则α∥β
其中正确命题有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.在△ABC中,角A、B、C所对边分别为a、b、c,若a2+b2=4a+6b-13,sinC=2sinA,则cosC的值为( )
| A. | -$\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{7}{8}$ | D. | $\frac{11}{16}$ |
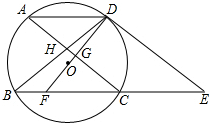 如图,⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E,AC∥DE交BD于点H,DO及延长线分别交AC,BC于点G,F.
如图,⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E,AC∥DE交BD于点H,DO及延长线分别交AC,BC于点G,F.