题目内容
5.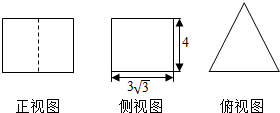 若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如图所示,则这个棱柱的表面积为$72+18\sqrt{3}$.则这个棱柱体积为36$\sqrt{3}$.
若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如图所示,则这个棱柱的表面积为$72+18\sqrt{3}$.则这个棱柱体积为36$\sqrt{3}$.
分析 由已知中的三视图,可得该几何体是一个正三棱柱,结合柱体的表面积和体积公式,可得答案.
解答 解:由已知中的三视图,可得该几何体是一个正三棱柱,
底面正三角形的高为3$\sqrt{3}$,故底面边长为6,
故底面面积为:$\frac{\sqrt{3}}{4}×{6}^{2}$=9$\sqrt{3}$,
棱柱的高为:4,
故棱柱的侧面积为:3×6×4=72,
故棱柱的表面积为:$72+18\sqrt{3}$;
棱柱体积为:36$\sqrt{3}$
故答案为:$72+18\sqrt{3}$,36$\sqrt{3}$
点评 本题考查的知识点是由三视图求体积和表面积,根据三视图判断出几何体的形状是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.若函数y=loga(x2-ax+$\frac{1}{2}$)有最小值,则a的取值范围是( )
| A. | 0<a<1 | B. | 0<a<$\sqrt{2}$,a≠1 | C. | 1<a<$\sqrt{2}$ | D. | a≥$\sqrt{2}$ |
17.在△ABC中,角A、B、C所对边分别为a、b、c,若a2+b2=4a+6b-13,sinC=2sinA,则cosC的值为( )
| A. | -$\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{7}{8}$ | D. | $\frac{11}{16}$ |
17.已知函数f(x)=-x2+ex-1(x≤1)与g(x)=ln(-x+a)的图象上存关于直线y=x-1对称的点,则a的取值范围是( )
| A. | (-∞,-2] | B. | [2,+∞) | C. | (-∞,2] | D. | [1,+∞) |
13.对于任意实数a,b,定义max{a,b}=$\left\{\begin{array}{l}{a,a≥b}\\{b,a<b}\end{array}\right.$,已知在[-2,2]上的偶函数f(x)满足当0≤x≤2时,f(x)=max{2x-1,2-x}若方程f(x)-mx+1=0恰有两个根,则m的取值范围是( )
| A. | [-2,-eln2)∪(eln2,2] | B. | [-eln2,0)∪(0,eln2] | C. | [-2,0)∪(0,2] | D. | [-e,-2)∪(2,e] |
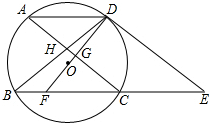 如图,⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E,AC∥DE交BD于点H,DO及延长线分别交AC,BC于点G,F.
如图,⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E,AC∥DE交BD于点H,DO及延长线分别交AC,BC于点G,F.