题目内容
已知{an}是单调递增的等差数列,首项a1=3,前n项和为Sn,等比数列{bn}的首项b1=1,且a2b2=12,S3+b2=20.
(1)求{an}和{bn}的通项公式;
(2)求{anbn}的前n项和Tn.
(1)求{an}和{bn}的通项公式;
(2)求{anbn}的前n项和Tn.
考点:等差数列与等比数列的综合
专题:等差数列与等比数列
分析:(1)设公差为d,公比为q,则a2b2=(3+d)q=12①,S3+b2=3a2+b2=3(3+d)+q=20②
联立①②结合d>0可求d,q,利用等差数列,等比数列的通项公式可求an,bn
(2)直接利用(1)的结论对数列{an•bn}用错位相减法求和即可求Tn.
联立①②结合d>0可求d,q,利用等差数列,等比数列的通项公式可求an,bn
(2)直接利用(1)的结论对数列{an•bn}用错位相减法求和即可求Tn.
解答:
解:(1)设公差为d,公比为q,
则a2b2=(3+d)q=12①
S3+b2=3a2+b2=3(3+d)+q=20②
联立①②可得,(3d+7)(d-3)=0
∵{an}是单调递增的等差数列,d>0.
则d=3,q=2,
∴an=3+(n-1)×3=3n,bn=2n-1…(6分)
(2)Tn=3•1+6•2+9•4+…+3n•2n-1,①
2Tn=3•2+6•4+9•8+…+3n•2n,②②-①得:Tn=-3(1+2+4+…+2n-1)+3n•2n-1
=-3(1+
)+3n•2n-1
=3(n-1)•2n-1
∴Tn=3(n-1)•2n-1.
则a2b2=(3+d)q=12①
S3+b2=3a2+b2=3(3+d)+q=20②
联立①②可得,(3d+7)(d-3)=0
∵{an}是单调递增的等差数列,d>0.
则d=3,q=2,
∴an=3+(n-1)×3=3n,bn=2n-1…(6分)
(2)Tn=3•1+6•2+9•4+…+3n•2n-1,①
2Tn=3•2+6•4+9•8+…+3n•2n,②②-①得:Tn=-3(1+2+4+…+2n-1)+3n•2n-1
=-3(1+
| 1-2n-1 |
| 1-2 |
=3(n-1)•2n-1
∴Tn=3(n-1)•2n-1.
点评:本题主要考查了利用基本量表示的等差数列、等比数列的通项,求和公式的应用,错位相减求解数列的和,属于数列的知识的综合应用,属于中档题.

练习册系列答案
相关题目
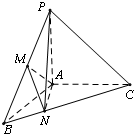 如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP,M为PB的中点,N在BC上,且BN=
如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP,M为PB的中点,N在BC上,且BN=| 1 |
| 3 |
(1)求证:MN⊥AB;
(2)求平面MAN与平面PAN的夹角的余弦值.
设f(x)=cos(
+
),则f(1)+f(2)+f(3)+…+f(2010)=( )
| nπ |
| 2 |
| π |
| 4 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
设集合M={x|x>
},则下面式子正确的是( )
| 3 |
| A、φ⊆M | ||
| B、0∈M | ||
C、-
| ||
| D、2∉M |