题目内容
已知数列{an}满足 a1=1,an=2an-1+1,(n>1)
(1)写出数列的前4项;
(2)求数列{an}的通项公式;
(3)求数列{an}的前n项和.
(1)写出数列的前4项;
(2)求数列{an}的通项公式;
(3)求数列{an}的前n项和.
考点:数列递推式,数列的求和
专题:点列、递归数列与数学归纳法
分析:(1)根据 a1=1,an=2an-1+1,写出前4项即可,
(2)由题意得an+1=2(an-1+1),继而得到{an+1}是以a1+1=1+1=2为首项,公比为2的等比数列,然后写出通项即可
(3)根基等比数列的求和公式计算即可
(2)由题意得an+1=2(an-1+1),继而得到{an+1}是以a1+1=1+1=2为首项,公比为2的等比数列,然后写出通项即可
(3)根基等比数列的求和公式计算即可
解答:
解:(1)a1=1,an=2an-1+1a2=2a1+1=3,------------1分
a3=2a2+1=7-------------2分
a4=2a3+1=15---------3分
(2)a1=1,an=2an-1+1,
∴an+1=2(an-1+1)-----------4分
=2-----------5分
∴{an+1}是以a1+1=1+1=2为首项,公比为2的等比数列,----6分
∴an+1=2×2n-1=2n-----------7分
∴an=2n-1-----------8分
(3)数列{an}的前n项和为Sn
则Sn=a1+a2+a3+a4+…+an
=(21-1)+(22-1)+(23-1)+(24-1)+…+(2n-1)---------10分
=(2+22+23+24+…+2n)-n------11分
=
-n---------13分
=2n+1-2-n---------14分.
a3=2a2+1=7-------------2分
a4=2a3+1=15---------3分
(2)a1=1,an=2an-1+1,
∴an+1=2(an-1+1)-----------4分
| an+1 |
| an-1+1 |
∴{an+1}是以a1+1=1+1=2为首项,公比为2的等比数列,----6分
∴an+1=2×2n-1=2n-----------7分
∴an=2n-1-----------8分
(3)数列{an}的前n项和为Sn
则Sn=a1+a2+a3+a4+…+an
=(21-1)+(22-1)+(23-1)+(24-1)+…+(2n-1)---------10分
=(2+22+23+24+…+2n)-n------11分
=
| 2-2n×2 |
| 1-2 |
=2n+1-2-n---------14分.
点评:本题考查数列的概念及数列的递推公式,及前n项公式,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
若l,m表示直线,α,β,γ表示平面,则下列命题不正确的是( )
| A、若l⊥m,l⊥α,m⊥β,则α⊥β |
| B、若l⊥m,l?α,m?β,则α⊥β |
| C、若α⊥γ,β∥γ,则α⊥β |
| D、若l∥m,l⊥α,m?β,则α⊥β |
已知α,β是平面,a,b,c是直线,O是点.下列五个命题:
①若α∥β,a?α,b?β,则a∥b;
②若a∥b,a⊥c,则b⊥c;
③若a∥α,b?α,则a∥b;
④若a∥α,b∥α,则a∥b;
⑤若a∩b=O,a∥α,则b与α平行或相交.
其中正确的有( )
①若α∥β,a?α,b?β,则a∥b;
②若a∥b,a⊥c,则b⊥c;
③若a∥α,b?α,则a∥b;
④若a∥α,b∥α,则a∥b;
⑤若a∩b=O,a∥α,则b与α平行或相交.
其中正确的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
方程2sin2x=x-3的解有( )个.
| A、1 | B、2 | C、3 | D、4 |
已知a>0且a≠1,下列四组函数中表示相等函数的是( )
| A、y=logax与y=(logxa)-1 |
| B、y=2x与y=logaa2x |
| C、y=alogax与y=x |
| D、y=logax2与y=2logax |
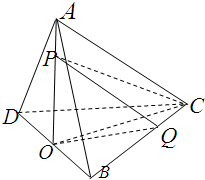 如图,在三棱锥A-BCD中,BC=DC=AB=AD=2,BD=2,平面ABD⊥平面BCD,O为BD中点,点P,Q分别为线段AO,BC上的动点(不含端点),且AP=CQ,则三棱锥P-QCO体积的最大值为
如图,在三棱锥A-BCD中,BC=DC=AB=AD=2,BD=2,平面ABD⊥平面BCD,O为BD中点,点P,Q分别为线段AO,BC上的动点(不含端点),且AP=CQ,则三棱锥P-QCO体积的最大值为
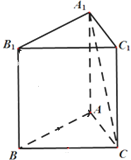 在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,AB=8,AC=6,BC=10.求证:
在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,AB=8,AC=6,BC=10.求证: