题目内容
已知点P是正方体ABCD-A1B1C1D1的表面上一动点,且满足|PA|=2|PB|,设PD1与平面ABCD所成角为θ,则θ的最大值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:直线与平面所成的角
专题:空间角
分析:先确定点P的轨迹,再利用正方体的几何性质解决.
解答:
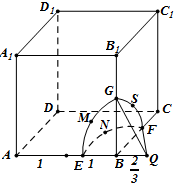 解:以B为原点,BC,BA,BB1,分别为x、y、z轴建立空间坐标系,设P(x,y,z),A(0,2,0),|PA|=2|PB|,∴
解:以B为原点,BC,BA,BB1,分别为x、y、z轴建立空间坐标系,设P(x,y,z),A(0,2,0),|PA|=2|PB|,∴
=
∴x2+(y+
)2+z2=
,∴点P的轨迹为:以点Q为球心,以半径为
的球与正方体表面的交线,即为如图的弧段EMG,GSF,FNE,
要使得PD1与底面ABCD所成角最大,则PD1与底面ABCD
的交点R与点D的距离最短,从而点P在弧段ENF上,故
点P在弧段ENF上,且在QD上.设正方体的边长为2,从而DQ=
-
=2,从而tanθ最大值为1,故θ最大值为
.
故选B
 解:以B为原点,BC,BA,BB1,分别为x、y、z轴建立空间坐标系,设P(x,y,z),A(0,2,0),|PA|=2|PB|,∴
解:以B为原点,BC,BA,BB1,分别为x、y、z轴建立空间坐标系,设P(x,y,z),A(0,2,0),|PA|=2|PB|,∴| (x-0)2+(y-2)2+(z-0)2 |
| x2+y2+z2 |
| 2 |
| 3 |
| 16 |
| 9 |
| 4 |
| 3 |
要使得PD1与底面ABCD所成角最大,则PD1与底面ABCD
的交点R与点D的距离最短,从而点P在弧段ENF上,故
点P在弧段ENF上,且在QD上.设正方体的边长为2,从而DQ=
| 10 |
| 3 |
| 4 |
| 3 |
| π |
| 4 |
故选B
点评:本题考查了动点的轨迹,线面角的定义,考查空间想象能力,逻辑思维能力,属中档题.

练习册系列答案
相关题目
已知函数f(x)=x3+ax+1是R上的单调递增函数,则a的取值范围是( )
| A、a≥0 | B、a≥-1 |
| C、a<0 | D、a<-1 |
已知双曲线
-x2=1与抛物线x2=ay有相同的焦点F,O为原点,点P是抛物线准线上一动点,点A在抛物线上,且|AF|=4,则|PA|+|PO|的最小值为( )
| y2 |
| 3 |
A、2
| ||
B、4
| ||
C、3
| ||
D、4
|
2sin
cos
的值是( )
| π |
| 12 |
| π |
| 12 |
A、
| ||
B、
| ||
C、
| ||
| D、1 |
设f(x)是定义在R上的奇函数,且f(x+3)•f(x)=-1,f(-1)=2,则f(2008)=( )
| A、0.5 | B、0 | C、2 | D、-1 |
若抛物线C1:y2=4x的焦点F恰好是双曲线C2:
-
=1(a>0,b>0)的右焦点,且C1与C2交点的连线过点F,则双曲线C2的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||||
B、2
| ||||||
C、3+2
| ||||||
D、
|
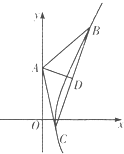 如图,B,C两点在双曲线x2-
如图,B,C两点在双曲线x2-