题目内容
已知函数f(x)=
x3-
(a+1)x2+ax
(1)a=-1时,求f(x)的单调区间;
(2)设a>0,x≥0,若f(x)>-
a恒成立,求a的取值范围.
| 1 |
| 3 |
| 1 |
| 2 |
(1)a=-1时,求f(x)的单调区间;
(2)设a>0,x≥0,若f(x)>-
| 2 |
| 3 |
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)a=-1时,f(x)=
x3-x,得f′(x)=(x+1)(x-1),从而f(x)在(-∞,-1),(1,+∞)递增,在(-1,1)递减;
(2)设a>0,x≥0,若f(x)>-
a恒成立,只需f(x)+
a>0即可,令g(x)=f(x)+
a=
x3-
(a+1)x2+ax+
a,得g′(x)=(x-a)(x-1),再分情况讨论①0<a<1时②a=1时③a>1时的a的范围,从而得出答案.
| 1 |
| 3 |
(2)设a>0,x≥0,若f(x)>-
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
解答:
解:(1)a=-1时,f(x)=
x3-x,
∴f′(x)=(x+1)(x-1),
令f′(x)>0,解得:x>1,x<-1,
令f′(x)<0,解得:-1<x<1,
∴f(x)在(-∞,-1),(1,+∞)递增,在(-1,1)递减;
(2)设a>0,x≥0,若f(x)>-
a恒成立,
只需f(x)+
a>0即可,
令g(x)=f(x)+
a=
x3-
(a+1)x2+ax+
a,
∴g′(x)=(x-a)(x-1),
①0<a<1时,g(x)在(0,a),(1,+∞)递增,在(a,1)递减,
∴g(x)最小值=g(x)极小值=g(1)=
-
(a+1)+a+
a>0,
解得:
<a<1,
②a=1时,g′(x)≥0,g(x)在[0,+∞)单调递增,
∴g(x)最小值=g(0)=
a>0,
③a>1时,f(x)在(0,1),(a,+∞)递增,在(1,a)递减,
∴只需g(x)最小值=g(x)极小值=g(a)=
a3-
(a+1)a2+a2+
a>0,
解得:1<a<4,
综合①②③得:a的取值范围是(
,4).
| 1 |
| 3 |
∴f′(x)=(x+1)(x-1),
令f′(x)>0,解得:x>1,x<-1,
令f′(x)<0,解得:-1<x<1,
∴f(x)在(-∞,-1),(1,+∞)递增,在(-1,1)递减;
(2)设a>0,x≥0,若f(x)>-
| 2 |
| 3 |
只需f(x)+
| 2 |
| 3 |
令g(x)=f(x)+
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
∴g′(x)=(x-a)(x-1),
①0<a<1时,g(x)在(0,a),(1,+∞)递增,在(a,1)递减,
∴g(x)最小值=g(x)极小值=g(1)=
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
解得:
| 1 |
| 7 |
②a=1时,g′(x)≥0,g(x)在[0,+∞)单调递增,
∴g(x)最小值=g(0)=
| 2 |
| 3 |
③a>1时,f(x)在(0,1),(a,+∞)递增,在(1,a)递减,
∴只需g(x)最小值=g(x)极小值=g(a)=
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
解得:1<a<4,
综合①②③得:a的取值范围是(
| 1 |
| 7 |
点评:本题考察了函数的单调性,导数的应用,渗透了数形结合思想,是一道中档题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
以双曲线
-
=1的右焦点为圆心,并与其渐近线相切的圆的标准方程是( )
| x2 |
| 64 |
| y2 |
| 36 |
| A、(x+10)2+y2=100 |
| B、(x-10)2+y2=64 |
| C、(x+10)2+y2=36 |
| D、(x-10)2+y2=36 |
设f(x)是定义在R上的奇函数,且f(x+3)•f(x)=-1,f(-1)=2,则f(2008)=( )
| A、0.5 | B、0 | C、2 | D、-1 |
若不等式组
表示的平面区域经过四个象限,则实数λ的取值范围是( )
|
| A、(-∞,2) |
| B、[-1,1] |
| C、[-1,2) |
| D、(1,+∞) |
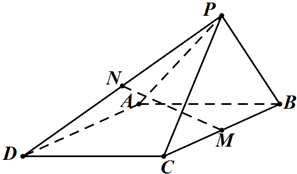 如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,∠ABC=60°,△PCB为正三角形,M,N分别为BC,PD的中点.
如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,∠ABC=60°,△PCB为正三角形,M,N分别为BC,PD的中点.