题目内容
设函数f（x）=2cos2x+2
sinxcosx-1（x∈R）．
（1）求函数f（x）的最小正周期；
（2）若0＜x≤
，求y=f（x）的值域．
| 3 |
（1）求函数f（x）的最小正周期；
（2）若0＜x≤
| π |
| 3 |
考点：三角函数中的恒等变换应用,三角函数的周期性及其求法
专题：常规题型,三角函数的图像与性质
分析：（1）先利用倍角公式及两角和的公式化成正弦型函数的标准形式，然后根据周期公式T=
求周期；（2）由x的范围先求出2x+
的范围，进而求出2sin(2x+
)的范围，得出函数y=f（x）的值域．
| 2π |
| |ω| |
| π |
| 6 |
| π |
| 6 |
解答：
解：（1）因为f（x）=2cos2x+2
sinxcosx-1
=1-cos2x+
sin2x-1
=2sin（2x+
）．
所以f（x）的最小正周期是T=
=π．
（2）∵0＜x≤
，∴
＜2x+
≤
+
=
，
∴
≤sin(2x+
)≤1
∴1≤2sin(2x+
)≤2，
故函数y=f（x）的值域为[1，2]．
| 3 |
=1-cos2x+
| 3 |
=2sin（2x+
| π |
| 6 |
所以f（x）的最小正周期是T=
| 2π |
| 2 |
（2）∵0＜x≤
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 2π |
| 3 |
| π |
| 6 |
| 5π |
| 6 |
∴
| 1 |
| 2 |
| π |
| 6 |
∴1≤2sin(2x+
| π |
| 6 |
故函数y=f（x）的值域为[1，2]．
点评：本题考查了三角变换及三角函数的周期性和值域问题，解题的关键是利用公式化成正弦型函数的标准形式．
练习册系列答案
阅读快车系列答案
相关题目
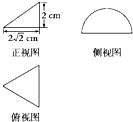一个几何体的三视图及其尺寸如图所示，其中正视图是直角三角形，侧视图是半圆，俯视图是等腰三角形，则这个几何体的表面积为（ ）A、2（1+2
| ||||
B、2（1+
| ||||
C、4（1+
| ||||
D、2（2+
|