题目内容
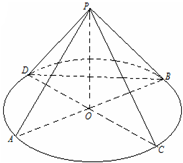 如图,AB,CD为圆O的两条直径,P为圆O所在平面外的一点,且PA=PB=PC
如图,AB,CD为圆O的两条直径,P为圆O所在平面外的一点,且PA=PB=PC(Ⅰ)求证:平面PAB⊥圆O所在平面;
(Ⅱ)若AP⊥BP,∠BAC=
| π |
| 6 |
考点:与二面角有关的立体几何综合题,平面与平面垂直的判定
专题:空间角
分析:(Ⅰ)由已知条件推导出△OPA≌△OPB≌△OPC,从而得到∠POA=∠POB=∠POC=
,由此能证明PO⊥圆O所在平面,从而得到平面PAB⊥圆O所在平面.
(Ⅱ)连接AC,BC,过C作CE⊥AB,垂足为E,过E作EF⊥BP,垂足为F,连接CF,由已知条件推导出∠EFC是二面角A-BP-C的平面角,由此能求出二面角A-PB-C的余弦值.
| π |
| 2 |
(Ⅱ)连接AC,BC,过C作CE⊥AB,垂足为E,过E作EF⊥BP,垂足为F,连接CF,由已知条件推导出∠EFC是二面角A-BP-C的平面角,由此能求出二面角A-PB-C的余弦值.
解答:
(Ⅰ)证明:∵AB,CD为圆O的两条直径,
P为圆O所在平面外的一点,且PA=PB=PC,
OP=OP=OP,
∴△OPA≌△OPB≌△OPC,
∴∠POA=∠POB=∠POC,
又∵∠POA+∠POB=π,
∴∠POA=∠POB=∠POC=
,
∵PO⊥AO,PO⊥CO,AO∩CO=O,
AO?圆O所在平面,CO?圆O所在平面,
∴PO⊥圆O所在平面,
∵PO?平面PAB,
∴平面PAB⊥圆O所在平面.
(Ⅱ)解:连接AC,BC,过C作CE⊥AB,垂足为E,
过E作EF⊥BP,垂足为F,连接CF,
由(Ⅰ)知PO⊥圆O所在平面,
∴PO⊥CE,
又∵AB⊥CE,PO∩AB=O,
∴CE⊥平面PAB,∴CE⊥BP,
又∵EF⊥BP,CE∩EF=E,∴BP⊥平面CEF,
∴BP⊥CF,BP⊥EF,
∴∠EFC是二面角A-BP-C的平面角,
设AB=2a,∵AB为圆O直径,C在圆O上,
∴AC⊥BC,又∵∠BAC=
,
∴AC=
a,BC=a,
又∵CE⊥AB,∠CBA=
,∴BE=
a,
∵AP⊥BP,AP=BP,∴△APB为等腰直角三角形,∴∠BAP=45°,
∴EF=
asin
=
a,
∴tan∠EFC=
=
=
,
∴cos∠EFC=
,
∴二面角A-PB-C的余弦值是
.
P为圆O所在平面外的一点,且PA=PB=PC,
OP=OP=OP,
∴△OPA≌△OPB≌△OPC,
∴∠POA=∠POB=∠POC,
又∵∠POA+∠POB=π,
∴∠POA=∠POB=∠POC=
| π |
| 2 |
∵PO⊥AO,PO⊥CO,AO∩CO=O,
AO?圆O所在平面,CO?圆O所在平面,
∴PO⊥圆O所在平面,
∵PO?平面PAB,
∴平面PAB⊥圆O所在平面.
(Ⅱ)解:连接AC,BC,过C作CE⊥AB,垂足为E,
过E作EF⊥BP,垂足为F,连接CF,
由(Ⅰ)知PO⊥圆O所在平面,
∴PO⊥CE,
又∵AB⊥CE,PO∩AB=O,
∴CE⊥平面PAB,∴CE⊥BP,
又∵EF⊥BP,CE∩EF=E,∴BP⊥平面CEF,
∴BP⊥CF,BP⊥EF,
∴∠EFC是二面角A-BP-C的平面角,
设AB=2a,∵AB为圆O直径,C在圆O上,
∴AC⊥BC,又∵∠BAC=
| π |
| 6 |
∴AC=
| 3 |
又∵CE⊥AB,∠CBA=
| π |
| 3 |
| 1 |
| 2 |
∵AP⊥BP,AP=BP,∴△APB为等腰直角三角形,∴∠BAP=45°,
∴EF=
| 1 |
| 2 |
| π |
| 4 |
| ||
| 4 |
∴tan∠EFC=
| CE |
| EF |
| ||||
|
| 6 |
∴cos∠EFC=
| ||
| 7 |
∴二面角A-PB-C的余弦值是
| ||
| 7 |
点评:本题考查平面与平面垂直的证明,考查二面角的余弦值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目