题目内容
已知f（x）=sinωx+
cosωx（ω＞0）的两条相邻的对称轴间的距离为
，且f（x）图象关于点（x0，0）成中心对称，则x0可能为（ ）
| 3 |
| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：利用两角和的正弦公式化简f（x），然后由f（x0）=0求得x0的值判断选项即可．
解答：
解：∵曲线f（x）=sin（ωx）+
cos（ωx）=2sin（ωx+
）的两条相邻的对称轴之间的距离为
，
∴
=π，
∴ω=2
∴f（x）=2sin（2x+
）．
∵f（x）的图象关于点（x0，0）成中心对称，
∴f（x0）=0，即2sin（2x0+
）=0，
∴2x0+
=kπ，
∴x0=
-
，k∈Z，
当k=1时，∴x0=
．
故选：C．
| 3 |
| π |
| 3 |
| π |
| 2 |
∴
| 2π |
| ω |
∴ω=2
∴f（x）=2sin（2x+
| π |
| 3 |
∵f（x）的图象关于点（x0，0）成中心对称，
∴f（x0）=0，即2sin（2x0+
| π |
| 3 |
∴2x0+
| π |
| 3 |
∴x0=
| kπ |
| 2 |
| π |
| 6 |
当k=1时，∴x0=
| π |
| 3 |
故选：C．
点评：本题考查两角和与差的正弦函数，考查了正弦函数的对称中心的求法，是中档题．
练习册系列答案
相关题目
Rt△ABC中CA=CB=
，M为AB的中点，将△ABC沿CM折叠，使A、B之间的距离为1，则三棱锥M-ABC外接球的表面积为（ ）
| 2 |
A、
| ||
| B、4π | ||
| C、3π | ||
D、
|
已知向量
与向量
的夹角为90°，且|
|=1，|
|=2，若
=
+λ
，
⊥（2
-
），则实数λ的值为（ ）
| a |
| b |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
A、λ=
| ||
B、λ=
| ||
C、λ=
| ||
| D、λ=1 |
若存在正实数M，对于任意x∈（1，+∞），都有|f（x）|≤M，则称函数f（x）在（1，+∞） 上是有界函数．下列函数：
①f（x）=
；
②f（x）=
；
③f（x）=
；
④f（x）=xsinx．
其中“在（1，+∞）上是有界函数”的序号为（ ）
①f（x）=
| 1 |
| x-1 |
②f（x）=
| x |
| x2+1 |
③f（x）=
| lnx |
| x |
④f（x）=xsinx．
其中“在（1，+∞）上是有界函数”的序号为（ ）
| A、②③ | B、①②③ |
| C、②③④ | D、③④ |
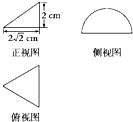一个几何体的三视图及其尺寸如图所示，其中正视图是直角三角形，侧视图是半圆，俯视图是等腰三角形，则这个几何体的表面积为（ ）A、2（1+2
| ||||
B、2（1+
| ||||
C、4（1+
| ||||
D、2（2+
|
已知F1，F2分别是双曲线C：
-
=1（a＞0，b＞0）的左、右焦点，点P在C的右支上，|PF1|，|PF2|，|F1F2|成等差数列，且∠PF1F2=120°，则该双曲线的离心率是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |