题目内容
设函数f(x)=x|x-a|,a>0
(1)若a=1时,判断f(x)的奇偶性;
(2)写出函数的单调区间;
(3)若关于x的方程f(x)=a-
在区间[1,2]上恰有两个不同的实数根,求实数a的取值范围.
(1)若a=1时,判断f(x)的奇偶性;
(2)写出函数的单调区间;
(3)若关于x的方程f(x)=a-
| 3 |
| 4 |
考点:函数奇偶性的性质,函数的单调性及单调区间,根的存在性及根的个数判断
专题:函数的性质及应用
分析:(1)求f(-1)=-2,f(1)=0,所以根据奇函数、偶函数的定义便知函数f(x)此时非奇非偶;
(2)去绝对值,然后根据二次函数的单调性即可写出函数f(x)的单调区间;
(3)可画出f(x)的图象,根据图象便容易求出a的取值范围.
(2)去绝对值,然后根据二次函数的单调性即可写出函数f(x)的单调区间;
(3)可画出f(x)的图象,根据图象便容易求出a的取值范围.
解答:
解:(1)若a=1,f(x)=x|x-1|;
f(-1)=-2,f(1)=0;
∴f(x)既不是奇函数,也不是偶函数;
(2)f(x)=x|x-a|=
;
∵a>0,∴x2-ax在[a,+∞)上单调递增;
-x2+ax在[
,a)上单调递减,在(-∞,
)上单调递增;
∴函数f(x)的单调增区间为(-∞,
),[a,+∞);
单调减区间为[
,a);
(3)f(x)的图象如下图所示:
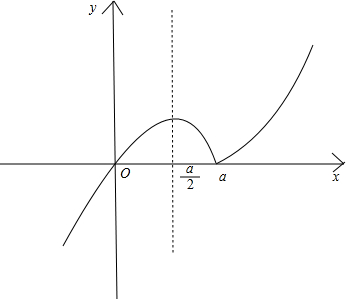 由图象知,符合题意的a应满足:
由图象知,符合题意的a应满足:
1<
<2,或1<a<2,即2<a<4,或1<a<2;
①当2<a<4时,则
;
解得3<a≤
;
②当1<a<2时,则
;
解得a∈∅;
∴综上得a的取值范围为(3,
].
f(-1)=-2,f(1)=0;
∴f(x)既不是奇函数,也不是偶函数;
(2)f(x)=x|x-a|=
|
∵a>0,∴x2-ax在[a,+∞)上单调递增;
-x2+ax在[
| a |
| 2 |
| a |
| 2 |
∴函数f(x)的单调增区间为(-∞,
| a |
| 2 |
单调减区间为[
| a |
| 2 |
(3)f(x)的图象如下图所示:
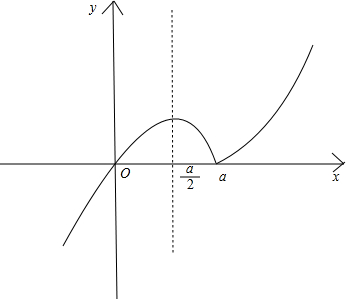 由图象知,符合题意的a应满足:
由图象知,符合题意的a应满足:1<
| a |
| 2 |
①当2<a<4时,则
|
解得3<a≤
| 13 |
| 4 |
②当1<a<2时,则
|
解得a∈∅;
∴综上得a的取值范围为(3,
| 13 |
| 4 |
点评:考查奇函数、偶函数的定义及判断方法,处理含绝对值函数的方法:去绝对值,二次函数的单调性,以及数形结合解题的方法.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案
相关题目
满足tanA>-1的三角形内角A的取值范围是( )
A、(0,
| ||||||
B、(0,
| ||||||
C、(
| ||||||
D、(0,
|
二项式(2x2-
)5的展开式中x的系数为( )
| 1 |
| x |
| A、-20 | B、20 |
| C、-40 | D、40 |
一个侧棱与底面垂直的四棱柱的正视图和俯视图如图所示,该四棱柱的体积为( )


A、
| ||||
B、
| ||||
C、
| ||||
D、
|
一物体的运动方程为s=
+2t(t>1),其中s的单位是米,t的单位是秒,那么物体在2秒末的瞬时速度是( )
| 1 |
| t |
A、
| ||
B、
| ||
C、
| ||
D、
|