题目内容
已知函数f(x)=
,若对任意x∈R,f(x)-|x-k|-|x-1|≤0恒成立,则实数k的取值范围是 .
|
考点:分段函数的应用
专题:计算题,数形结合,分类讨论,函数的性质及应用
分析:求出y=f(x)-|x-1|,在直角坐标系中,画出函数y=f(x)-|x-1|和y=|x-k|的图象,讨论k=1,k=
,两图象的关系,运用作差比较即可判断;再由图象平移,通过观察即可判断k>1或k<
也成立,即可得到k的范围.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
 解:y=f(x)-|x-1|=
解:y=f(x)-|x-1|=
,
在直角坐标系中,画出函数y=f(x)-|x-1|和y=|x-k|的图象,
①当k=1时,它们都过(1,0),当x<1时,y=|x-1|=1-x,
y=f(x)-|x-1|=-2x2+3x-1,由1-x-(-2x2+3x-1)=2x2-4x+2
=2(x-1)2>0,则有x≤1时,f(x)-|x-k|-|x-1|≤0恒成立,x>1由图象可得f(x)-|x-k|-|x-1|≤0恒成立;
②当k=
时,它们都过(
,0),当x>
,y=|x-
|=x-
,
由于x>1时,f(x)<0,只要考虑
<x<1,y=f(x)-|x-1|=-2x2+3x-1,
由x-
-(-2x2+3x-1)=2x2-2x+
=2(x-
)2>0,则有
<x<1,f(x)-|x-k|-|x-1|≤0恒成立,
x>1或x<
时,由图象可得,f(x)-|x-k|-|x-1|≤0恒成立,
则k=1,
时,对任意x∈R,f(x)-|x-k|-|x-1|≤0恒成立;
③当k>1或k<
时,由图象平移可得,对任意x∈R,f(x)-|x-k|-|x-1|≤0恒成立.
综上可得,k的取值范围为k≥1或k≤
.
故答案为:(-∞,
]∪[1,+∞).
 解:y=f(x)-|x-1|=
解:y=f(x)-|x-1|=
|
在直角坐标系中,画出函数y=f(x)-|x-1|和y=|x-k|的图象,
①当k=1时,它们都过(1,0),当x<1时,y=|x-1|=1-x,
y=f(x)-|x-1|=-2x2+3x-1,由1-x-(-2x2+3x-1)=2x2-4x+2
=2(x-1)2>0,则有x≤1时,f(x)-|x-k|-|x-1|≤0恒成立,x>1由图象可得f(x)-|x-k|-|x-1|≤0恒成立;
②当k=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由于x>1时,f(x)<0,只要考虑
| 1 |
| 2 |
由x-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
x>1或x<
| 1 |
| 2 |
则k=1,
| 1 |
| 2 |
③当k>1或k<
| 1 |
| 2 |
综上可得,k的取值范围为k≥1或k≤
| 1 |
| 2 |
故答案为:(-∞,
| 1 |
| 2 |
点评:本题考查分段函数及运用,考查数形结合的思想方法,考查图象的平移规律,考查分类讨论的数学思想,考查运算能力,属于中档题和易错题.

练习册系列答案
相关题目
甲乙两名运动员在某项测试中的8次成绩如茎叶图所示,则甲运动员的极差与乙运动员的众数分别是( )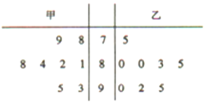

| A、20、80 |
| B、20、81 |
| C、17、80 |
| D、17、81 |
 某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数,按十位数学为茎,个位数学为叶得到的茎叶图如图所示,已知甲、乙两组数据的平均数都为10.
某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数,按十位数学为茎,个位数学为叶得到的茎叶图如图所示,已知甲、乙两组数据的平均数都为10.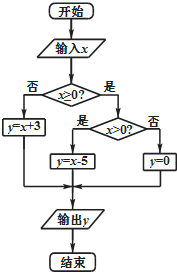 执行如图所示的程序框图,在集合A={x∈R|-10≤x≤10}中随机地取一个数值作为x输入,则输出的y值落在区间(-5,3)内的概率为( )
执行如图所示的程序框图,在集合A={x∈R|-10≤x≤10}中随机地取一个数值作为x输入,则输出的y值落在区间(-5,3)内的概率为( )