题目内容
已知直线l:2x+y+4=0与圆C:x2+y2+2x-4y+1=0相交于A,B两点,求:
(1)线段AB的长;
(2)以AB为直径的圆M的标准方程.
(1)线段AB的长;
(2)以AB为直径的圆M的标准方程.
考点:直线与圆相交的性质
专题:直线与圆
分析:(1)先将圆化为标准方程,然后利用点到直线的距离求弦长;
(2)联立直线方程和圆的方程,利用根与系数之间的关系求出A,B的中点坐标即可求出以AB为直径的圆M的标准方程.
(2)联立直线方程和圆的方程,利用根与系数之间的关系求出A,B的中点坐标即可求出以AB为直径的圆M的标准方程.
解答:
解:(1)圆的标准方程为(x+1)2+(y-2)2=4,圆心为P(-1,2),半径为r=2.
所以圆心到直线的距离d=
=
.
所以弦长l=2
=2
=2
=
=
.
故线段AB的长为
;
(2)∵|AB|=
,∴以AB为直径的圆的半径为
,
由2x+y+4=0得y=-2x-4代入圆的方程得5x2+26x+33=0,
则x1+x2=-
,即中点横坐标x=
(x1+x2)=-
,
纵坐标y=-2x-4=
,即圆心坐标为(-
,
),
则以AB为直径的圆的方程为(x+
)2+(y-
)2=(
)2=
.
所以圆心到直线的距离d=
| |-2+2+4| | ||
|
| 4 | ||
|
所以弦长l=2
| r2-d2 |
4-
|
|
| 4 | ||
|
4
| ||
| 5 |
故线段AB的长为
4
| ||
| 5 |
(2)∵|AB|=
4
| ||
| 5 |
2
| ||
| 5 |
由2x+y+4=0得y=-2x-4代入圆的方程得5x2+26x+33=0,
则x1+x2=-
| 26 |
| 5 |
| 1 |
| 2 |
| 13 |
| 5 |
纵坐标y=-2x-4=
| 6 |
| 5 |
| 13 |
| 5 |
| 6 |
| 5 |
则以AB为直径的圆的方程为(x+
| 13 |
| 5 |
| 6 |
| 5 |
2
| ||
| 5 |
| 4 |
| 5 |
点评:本题主要考查直线和圆的方程的应用,根据弦长公式以及联立直线和圆的方程,结合根与系数之间的关系是解决本题的关键.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
函数f(x)=3x+lnx-5的零点所在区间为( )
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
双曲线3x2-4y2=-12的焦点为F1、F2,则( )
| A、F1(5,0),F2(-5),0 | ||||
B、F1(
| ||||
C、F1(0,
| ||||
| D、F1(1,0),F2(-1,0) |
甲乙两名运动员在某项测试中的8次成绩如茎叶图所示,则甲运动员的极差与乙运动员的众数分别是( )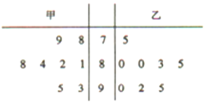

| A、20、80 |
| B、20、81 |
| C、17、80 |
| D、17、81 |
设函数f(x)=x|x-a|,a>0
(1)若a=1时,判断f(x)的奇偶性;
(2)写出函数的单调区间;
(3)若关于x的方程f(x)=a-
在区间[1,2]上恰有两个不同的实数根,求实数a的取值范围.
(1)若a=1时,判断f(x)的奇偶性;
(2)写出函数的单调区间;
(3)若关于x的方程f(x)=a-
| 3 |
| 4 |
函数f(x)满足对定义域内的任意x,都有f(x+2)+f(x)<2f(x+1),则函数f(x)可以是( )
| A、f(x)=2x+1 |
| B、f(x)=x2-2x |
| C、f(x)=ex |
| D、f(x)=lnx |