题目内容
两圆相交于点A(1,3)、B(m,-1),两圆的圆心均在直线x-y+c=0上,则m+c的值为( )
| A、-1 | B、2 | C、0 | D、3 |
考点:圆与圆的位置关系及其判定
专题:直线与圆
分析:由已知中两圆相交于点A(1,3)、B(m,-1),两圆的圆心均在直线x-y+c=0上,我们易得到直线x-y+c=0为线段AB的垂直平分线,即直线AB与直线x-y+c=0的斜率乘积为-1,且AB的中点落在直线x-y+c=0上,求出m,c后,即可得到答案.
解答:
解:∵两圆的圆心均在直线x-y+c=0上,则直线x-y+c=0为线段AB的垂直平分线,
即KAB=-1=
,解得m=5.
由AB的中点(3,1)在直线x-y+c=0上,可得3-1+c=0,解得c=-2,∴m+c=3,
故答案为:3.
即KAB=-1=
| 3+1 |
| 1-m |
由AB的中点(3,1)在直线x-y+c=0上,可得3-1+c=0,解得c=-2,∴m+c=3,
故答案为:3.
点评:本题考查的知识点是圆与圆的位置关系,直线与直线垂直的斜率关系,其中根据已知判断出直线x-y+c=0为线段AB的垂直平分线,是解答本题的关键,属于基础题.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
某三棱锥的三视图如图所示,则该三棱锥的体积是( )


| A、1 | ||
B、
| ||
C、
| ||
D、
|
设f(x)=2x-3,g(x+2)=f(x),则g(x)=( )
| A、2x+1 | B、2x+3 |
| C、2x-7 | D、2x-3 |
过点(-2,0),且与直线3x-y+1=0平行的直线方程式( )
| A、y=3x-6 |
| B、y=3x+6 |
| C、y=3x-2 |
| D、y=-3x-6 |
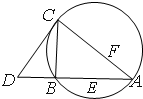 如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E,F分别为弦AB与弦AC上的点,且BC•AE=DC•AF,B,E,F,C四点共圆.
如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E,F分别为弦AB与弦AC上的点,且BC•AE=DC•AF,B,E,F,C四点共圆.