题目内容
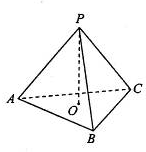
某三棱锥的三视图如图所示,则该三棱锥的体积是( )


| A、1 | ||
B、
| ||
C、
| ||
D、
|
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由三视图可知:该几何体是一个以俯视图为底面的三棱锥,求出底面面积和高,进而可得该几何体的体积.
解答:
解:由三视图可知:该几何体是一个以俯视图为底面的三棱锥,
底面的两条直角边均为1,
底面面积S=
×1×1=
,
高h=2,
故棱锥的体积V=
Sh=
,
故选:D
底面的两条直角边均为1,
底面面积S=
| 1 |
| 2 |
| 1 |
| 2 |
高h=2,
故棱锥的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
故选:D
点评:本题考查的知识点是由三视图求几何体的体积或表面积,由三视图正确恢复原几何体是解题的关键.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
圆心为(1,-1),半径为2的圆的方程是( )
| A、(x-1)2+(y+1)2=2 |
| B、(x-1)2+(y-1)2=4 |
| C、(x+1)2+(y-1)2=2 |
| D、(x-1)2+(y+1)2=4 |
样本11、12、13、14、15的方差是( )
| A、13 | B、10 | C、2 | D、4 |
椭圆与双曲线
-
=1有相同的焦点且离心率为
,则椭圆的标准方程为( )
| x2 |
| 3 |
| y2 |
| 2 |
| 1 | ||
|
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
两圆相交于点A(1,3)、B(m,-1),两圆的圆心均在直线x-y+c=0上,则m+c的值为( )
| A、-1 | B、2 | C、0 | D、3 |
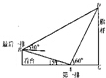 某中学举行升旗仪式,如图所示,在坡度为15°的看台上,从正对旗杆的一列的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离AB=10
某中学举行升旗仪式,如图所示,在坡度为15°的看台上,从正对旗杆的一列的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离AB=10