题目内容
17. 如图,在直三棱柱ABC-A1B1C1中,底面△ABC是等腰直角三角形,且斜边AB=$\sqrt{2}$,侧棱AA1=2,点D为AB的中点,点E在线段AA1上,AE=λAA1(λ为实数).
如图,在直三棱柱ABC-A1B1C1中,底面△ABC是等腰直角三角形,且斜边AB=$\sqrt{2}$,侧棱AA1=2,点D为AB的中点,点E在线段AA1上,AE=λAA1(λ为实数).(1)求证:不论λ取何值时,恒有CD⊥B1E;
(2)当λ=$\frac{1}{3}$时,求多面体C1B-ECD的体积.
分析 (1)由已知可得CD⊥AB.再由AA1⊥平面ABC,得AA1⊥CD.利用线面垂直的判定可得CD⊥平面ABB1A1.进一步得到CD⊥B1E;
(2)当λ=$\frac{1}{3}$时,$AE=\frac{1}{3}A{A}_{1}=\frac{2}{3}$.再由△ABC是等腰直角三角形,且斜边$AB=\sqrt{2}$,得AC=BC=1.然后利用${V}_{{C}_{1}B-ECD}={V}_{{C}_{1}-BCE}+{V}_{D-BCE}$结合等积法得答案.
解答 (1)证明:∵△ABC是等腰直角三角形,点D为AB的中点,∴CD⊥AB.
∵AA1⊥平面ABC,CD?平面ABC,∴AA1⊥CD.
又∵AA1?平面ABB1A1,AB?平面ABB1A1,AA1∩AB=A,
∴CD⊥平面ABB1A1.
∵点E在线段AA1上,∴B1E?平面ABB1A1,
∴CD⊥B1E;
(2)解:当λ=$\frac{1}{3}$时,$AE=\frac{1}{3}A{A}_{1}=\frac{2}{3}$.
∵△ABC是等腰直角三角形,且斜边$AB=\sqrt{2}$,∴AC=BC=1.
∴${V_{{C_1}-CBE}}={V_{E-{C_1}BC}}=\frac{1}{3}AC•{S_{△{C_1}BC}}=\frac{1}{3}×\frac{1}{2}×1×1×2=\frac{1}{3}$,
${V_{D-BEC}}={V_{E-CDB}}=\frac{1}{3}AE•{S_{△DBC}}=\frac{1}{3}×\frac{1}{2}×\frac{1}{2}×1×1×\frac{2}{3}=\frac{1}{18}$,
∴$V=\frac{1}{3}+\frac{1}{18}=\frac{7}{18}$.
点评 本题考查线面垂直的判定和性质,考查空间想象能力和思维能力,训练了利用等积法求得多面体的体积,是中档题.

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案| A. | $-\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{4}$ | D. | 1 |
| A. | 6π | B. | ($\sqrt{2}$+$\sqrt{5}$+1)π | C. | (2$\sqrt{2}$+2$\sqrt{5}$)π | D. | ($\sqrt{2}$+$\sqrt{5}$)π |
| A. | 命题¬p是真命题 | |
| B. | 命题p是特称命题 | |
| C. | 命题p是全称命题 | |
| D. | 命题p既不是全称命题也不是特称命题 |
| A. | $f(x)=-f({x+\frac{π}{2}})$ | B. | $f(x)=f({-x+\frac{π}{2}})$ | C. | $f(x)•f({x+\frac{π}{2}})=1$ | D. | $f(x)=-f({-x+\frac{π}{2}})$ |
| A. | 4 | B. | 8 | C. | 16 | D. | 32 |
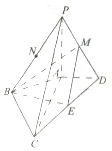 在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD,PA=AC=2AD=4,AB=BC=2$\sqrt{5}$,M,N,E分别为PD,PB,CD的中点.
在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD,PA=AC=2AD=4,AB=BC=2$\sqrt{5}$,M,N,E分别为PD,PB,CD的中点.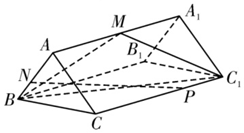 如图,已知三棱柱ABC-A1B1C1的底面ABC是等边三角形,且AA1⊥底面ABC,M为AA1的中点,N在线段AB上,且AN=2NB,点P在CC1上.
如图,已知三棱柱ABC-A1B1C1的底面ABC是等边三角形,且AA1⊥底面ABC,M为AA1的中点,N在线段AB上,且AN=2NB,点P在CC1上.