题目内容
16.过双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右焦点F的直线l:y=$\sqrt{3}x-4\sqrt{3}$与C只有一个公共点,则C的焦距为8,C的离心率为2.分析 结合双曲线的性质$\frac{b}{a}$=$\sqrt{3}$,0=$\sqrt{3}$c-4$\sqrt{3}$,求出a,c即可.
解答 解:过双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的渐近线方程为y=±$\frac{b}{a}$x,
因为过双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右焦点F的直线l:y=$\sqrt{3}x-4\sqrt{3}$与C只有一个公共点,
所以$\frac{b}{a}$=$\sqrt{3}$,0=$\sqrt{3}$c-4$\sqrt{3}$,
又因为a2+b2=c2,
解得c=3,a=$\frac{3}{2}$,
所以2c=8,e=$\frac{c}{a}$=2,
故答案为:8,2
点评 本题给出双曲线方程,求经过双曲线的右交点且与双曲线只有一个公共点的直线的条数.着重考查了直线的方程、双曲线的标准方程与简单几何性质等知识,属于中档题.

练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
4.已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的最小正周期为π,且其图象向右平移$\frac{π}{6}$个单位后得到函数g(x)=sinωx的图象,则φ等于( )
| A. | -$\frac{π}{3}$ | B. | -$\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
11.某宣传部门网站为弘扬社会主义思想文化,开展了以核心价值观为主题的系列宣传活动,并以“社会主义核心价值观”作为关键词便于网民搜索.此后,该网站的点击量每月都比上月增长50%,那么4个月后,该网站的点击量和原来相比,增长为原来的( )
| A. | 2倍以上,但不超过3倍 | B. | 3倍以上,但不超过4倍 | ||
| C. | 4倍以上,但不超过5倍 | D. | 5倍以上,但不超过6倍 |
8.不等式组$\left\{\begin{array}{l}x≥2\\ x+y≥6\\ x-2y≤0\end{array}\right.$所表示的平面区域为Ω,若直线ax-y+a+1=0与Ω有公共点,则实数a的最小值为( )
| A. | $-\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{4}$ | D. | 1 |
5.在平面直角坐标系xOy中,将不等式组$\left\{\begin{array}{l}{x-y+1≥0}\\{x+2y-2≤0}\\{y≥0}\end{array}\right.$表示的平面区域绕x轴旋转一周所形成的几何体的表面积是( )
| A. | 6π | B. | ($\sqrt{2}$+$\sqrt{5}$+1)π | C. | (2$\sqrt{2}$+2$\sqrt{5}$)π | D. | ($\sqrt{2}$+$\sqrt{5}$)π |
6.若等比数列{an}的前n项和${S_n}={2^{n-1}}+a$,则a3a5=( )
| A. | 4 | B. | 8 | C. | 16 | D. | 32 |




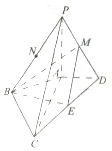 在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD,PA=AC=2AD=4,AB=BC=2$\sqrt{5}$,M,N,E分别为PD,PB,CD的中点.
在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD,PA=AC=2AD=4,AB=BC=2$\sqrt{5}$,M,N,E分别为PD,PB,CD的中点.