题目内容
若随机变量X～N（2，σ2），若X在（0，2）上的概率为0.2，则X在（-∞，4]的概率等于（ ）
| A、0.2 | B、0.3 |
| C、0.7 | D、0.9 |
考点：正态分布曲线的特点及曲线所表示的意义
专题：计算题,概率与统计
分析：由随机变量X～N（2，σ2）知，X的均值为2，其图象关于x=2对称，因为X在（0，2）内取值的概率为0.2，所以X在（2，4）内取值的概率为0.2，而且X在（-∞，0）和（4，+∞）内的概率相等，故可求X在（-∞，4]内的概率．
解答：
解：由随机变量X～N（2，σ2）知，X的均值为2，其图象关于x=2对称，
故X在（4，+∞）内的概率为P=
（1-0.2×2）=0.3，
∴X在（-∞，4]的概率等于1-0.3=0.7
故选：C．
故X在（4，+∞）内的概率为P=
| 1 |
| 2 |
∴X在（-∞，4]的概率等于1-0.3=0.7
故选：C．
点评：本题考查正态分布、由正态密度曲线的对称性求概率，属基本知识的考查．
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
小学期末标准试卷系列答案
相关题目
阅读如图的程序框图，运行相应的程序，则输出S的值为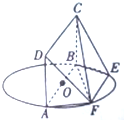
如图，AB为圆O的直径，四边形ABCD为正方形，点E、F在圆O上，AD⊥AF，AB=4，EF=AF=2
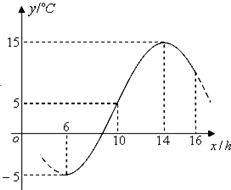如图，某地一天6-16时的温度变化曲线近似满足函数y=Asin（ωx+φ）+b，其中A＞0，ω＞0，0＜φ＜π．已知平面向量
=（1，2），
=（x，1），如果向量
+2
与2
-
平行，那么
•（
-
）等于（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| A、-2 | ||
| B、-1 | ||
C、
| ||
D、
|