题目内容
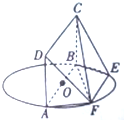 如图,AB为圆O的直径,四边形ABCD为正方形,点E、F在圆O上,AD⊥AF,AB=4,EF=AF=2
如图,AB为圆O的直径,四边形ABCD为正方形,点E、F在圆O上,AD⊥AF,AB=4,EF=AF=2(1)求证:EF∥平面ABCD;
(2)求三棱锥B-CEF的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)由已知得∠AFB=90°,∠ABF=∠EBF=30°,从而OB=OE=BE=AF=2,进而EF∥AB,由此能证明EF∥平面ABCD.
(2)由已知得CB⊥平面BEF,且CB=4,又S△BEF=
×BE×EF×sin∠BEF,再由VB-CEF=VC-BEF,能求出三棱锥B-CEF的体积.
(2)由已知得CB⊥平面BEF,且CB=4,又S△BEF=
| 1 |
| 2 |
解答:
(1)证明:∵AB为圆O的直径,四边形ABCD为正方形,
点E、F在圆O上,AD⊥AF,AB=4,EF=AF=2,
∴∠AFB=90°,∠ABF=∠EBF=30°,
∴OB=OE=BE=AF=2,
∴∠ABF=∠EFB=30°,∴EF∥AB,
又AB?平面ABCD,EF?平面ABCD,
∴EF∥平面ABCD.
(2)解:∵四边形ABCD为正方形,点E、F在圆O上,AD⊥AF,
∴CB⊥平面BEF,且CB=4,
又S△BEF=
×BE×EF×sin∠BEF
=
×2×2×sin120°=
,
∴VB-CEF=VC-BEF=
S△BEF•CB=
×
×4=
.

点E、F在圆O上,AD⊥AF,AB=4,EF=AF=2,
∴∠AFB=90°,∠ABF=∠EBF=30°,
∴OB=OE=BE=AF=2,
∴∠ABF=∠EFB=30°,∴EF∥AB,
又AB?平面ABCD,EF?平面ABCD,
∴EF∥平面ABCD.
(2)解:∵四边形ABCD为正方形,点E、F在圆O上,AD⊥AF,
∴CB⊥平面BEF,且CB=4,
又S△BEF=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 3 |
∴VB-CEF=VC-BEF=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
4
| ||
| 3 |
点评:本题考查直线与平面平行的证明,考查三棱锥的体积的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
已知直三棱柱ABC-A1B1C1的6个顶点都在球O的球面上,若AB=1,AC=2,BC=
,AA1=
,则球O的表面积为:( )
| 5 |
| 11 |
A、
| ||
| B、18π | ||
| C、32π | ||
| D、16π |
若随机变量X~N(2,σ2),若X在(0,2)上的概率为0.2,则X在(-∞,4]的概率等于( )
| A、0.2 | B、0.3 |
| C、0.7 | D、0.9 |
已知函数f(x)=sin(2x+φ)在区间[
,
]上单调递减,则实数φ的取值可以是( )
| π |
| 3 |
| 5π |
| 6 |
A、-
| ||
B、
| ||
C、
| ||
D、
|
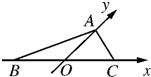
 如图,直角△ABC,∠A=90°,BC=2AB,AH⊥BC,BH=1,点M在AH上,且AH=3AM,则
如图,直角△ABC,∠A=90°,BC=2AB,AH⊥BC,BH=1,点M在AH上,且AH=3AM,则