题目内容
7. 运行如图程序框图.
运行如图程序框图.(1)当输入x值等于-1时,求输出y的值;
(2)当输出y的值最大值时,求输入x的值.
分析 (1)由已知中的程序框图可知:该程序的功能是利用条件结构计算并输出分段函数,计算x=-1时y的值即可,
(2)结合函数的单调性,可得答案.
解答 解:(1)由已知中的程序框图可知:
该程序的功能是利用条件结构计算并输出分段函数:
y=$\left\{\begin{array}{l}{{-x}^{2},x>0}\\{x+1{-e}^{x},x≤0}\end{array}\right.$ 的值,
当输入x=-1时,y=-$\frac{1}{e}$;
(2)∵y′=$\left\{\begin{array}{l}{-2x,x>0}\\{1{-e}^{x},x≤0}\end{array}\right.$,
故当x∈(-∞,0]时,y′≥0恒成立,函数为增函数;
当x∈(0,+∞)时,y′<0恒成立,函数为减函数;
∴当x=0时,y取最大值.
点评 本题考查的知识点是程序框图,函数的单调性,分段函数的应用,难度中档.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
17.集合M={x|x=3n,n∈N},集合N={x|x=3n,n∈N},则集合M与集合N的关系( )
| A. | M⊆N | B. | N⊆M | C. | M∩N=∅ | D. | M?N且N?M |
15.下列函数中,定义域为R的偶函数是( )
| A. | y=$\sqrt{{x}^{2}-1}$ | B. | y=ex-e-x | C. | y=ln|x| | D. | y=x${\;}^{\frac{2}{3}}$ |
2.若方程lnx+x=3在区间(a,a+1)(a∈N)上恰有一根,则a的值是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
12.2016年1月1日起全国统一实施全面两孩政策,为了解适龄民众对放开生育二胎政策的态度,某市选取70后,80后作为调查对象,随机调查了100位,得到数据如表:
(1)根据调查数据,判断是否有90%以上把握认为“生二胎与年龄有关”,并说明理由,参考数据如下:
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,n=a+b+c+d.
(2)以选100人的样本数据估计该市的总体数据,且以频率估计概率,若从该市70后公民中(人数很多)随机抽取3位,求3人中生二胎的人数为1人的概率.
| 生二胎 | 不生二胎 | 合计 | |
| 70后 | 30 | 15 | 45 |
| 80后 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
| P(k2≥k | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
(2)以选100人的样本数据估计该市的总体数据,且以频率估计概率,若从该市70后公民中(人数很多)随机抽取3位,求3人中生二胎的人数为1人的概率.
16. 如图是一个正三棱柱挖去一个圆柱得到的一个几何体的三视图,则该几何体的体积与挖去的圆柱的体积比为( )
如图是一个正三棱柱挖去一个圆柱得到的一个几何体的三视图,则该几何体的体积与挖去的圆柱的体积比为( )
 如图是一个正三棱柱挖去一个圆柱得到的一个几何体的三视图,则该几何体的体积与挖去的圆柱的体积比为( )
如图是一个正三棱柱挖去一个圆柱得到的一个几何体的三视图,则该几何体的体积与挖去的圆柱的体积比为( )| A. | $\frac{{3\sqrt{3}}}{π}-1$ | B. | $\frac{{3\sqrt{3}}}{π}-\frac{1}{3}$ | C. | $\frac{{3\sqrt{3}}}{π}$ | D. | $\frac{{3\sqrt{3}}}{π}+1$ |
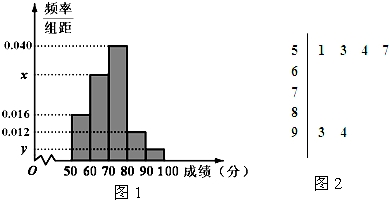
 某厂商调查甲、乙两种不同型号电视在10个卖场的销售量(单位:台),并根据这10个卖场的销售情况,得到如图所示的茎叶图.为了鼓励卖场,在同型号电视机的销售中,该厂商将销售量高于数据平均数的卖场命名为该型号电视机的“星级卖场”
某厂商调查甲、乙两种不同型号电视在10个卖场的销售量(单位:台),并根据这10个卖场的销售情况,得到如图所示的茎叶图.为了鼓励卖场,在同型号电视机的销售中,该厂商将销售量高于数据平均数的卖场命名为该型号电视机的“星级卖场”