题目内容
17．集合M={x|x=3n，n∈N}，集合N={x|x=3n，n∈N}，则集合M与集合N的关系（ ）| A． | M⊆N | B． | N⊆M | C． | M∩N=∅ | D． | M?N且N?M |
分析 利用子集的定义判断两个集合间的包含关系，从而确定集合间的关系．
解答 解：∵1∈M，1∉N；
0∈N，0∉M；
∴M?N且N?M．
故选：D．
点评 本题考查了子集的定义及集合间关系的判断，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
8．已知直线l1：（k+1）x+y+1=0和l2：（k-3）x-ky-1=0，若l1与l2有公共点，则k的取值范围为（ ）
| A． | k≠1且k≠-3 | B． | k≠-3 | C． | k=1 | D． | k=1且k=-3 |
12．
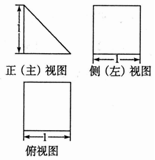某几何体的三视图如图所示，则该几何体的体积为（ ）
某几何体的三视图如图所示，则该几何体的体积为（ ）| A． | $\frac{1}{2}$ | B． | 1 | C． | $\frac{3}{2}$ | D． | 2 |
2．设集合A={1，2，3，4}，B={3，4，5}，则集合A∩B=（ ）
| A． | {1，2，4} | B． | {1，2，5} | C． | {3，4} | D． | {3，4，5} |
9．在正方体ABCD-A1B1C1D1中，直线BB1与平面ACD1所成角的余弦值为（ ）
| A． | $\frac{\sqrt{6}}{3}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{\sqrt{2}}{3}$ |
运行如图程序框图．