题目内容
2．若方程lnx+x=3在区间（a，a+1）（a∈N）上恰有一根，则a的值是（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 设函数f（x）=lnx+x-3，判断解的区间，即可得到结论．
解答 解：设函数f（x）=lnx+x-3，则函数f（x）单调递增，
∵f（2）=ln2+2-3=ln2-1＜0，f（3）=ln3+3-3=ln3＞0，
∴f（2）f（3）＜0，
在区间（2，3）内函数f（x）存在零点，
∵方程lnx+x=3在区间（a，a+1）（a∈N）上恰有一根，
∴a=2，
故选：B．
点评 本题主要考查方程根的存在性，根据方程构造函数，利用函数零点的条件判断，零点所在的区间是解决本题的关键．
练习册系列答案
相关题目
12．
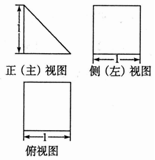某几何体的三视图如图所示，则该几何体的体积为（ ）
某几何体的三视图如图所示，则该几何体的体积为（ ）| A． | $\frac{1}{2}$ | B． | 1 | C． | $\frac{3}{2}$ | D． | 2 |
如图，CD为△ABC外接圆的切线，AB的延长线交直线CD于点D，E，F分别为弦AB与弦AC上的点，且BC•AE=DC•AF，B，E，F，C四点共圆．证明：CA是△ABC外接圆的直径．
17．
若执行如图所示的程序图，则运行后输出的结果是（ ）
若执行如图所示的程序图，则运行后输出的结果是（ ）| A． | 3 | B． | -3 | C． | -2 | D． | 2 |
运行如图程序框图．
14．已知向量$\overrightarrow a=（{1，2}），\overrightarrow b=（{-3，2}）$，若$（{k\overrightarrow a+\overrightarrow b}）∥（{\overrightarrow a-3\overrightarrow b}）$，则实数k的值为（ ）
| A． | 3 | B． | $\frac{1}{3}$ | C． | $-\frac{1}{3}$ | D． | -3 |
微信运动和运动手环的普及，增强了人民运动的积极性，每天一万步称为一种健康时尚，某中学在全校范围内内积极倡导和督促师生开展“每天一万步”活动，经过几个月的扎实落地工作后，学校想了解全校师生每天一万步的情况，学校界定一人一天走路不足4千步为不健康生活方式，不少于16千步为超健康生活方式者，其他为一般生活方式者，学校委托数学组调查，数学组采用分层抽样的办法去估计全校师生的情况，结合实际及便于分层抽样，认定全校教师人数为200人，高一学生人数为700人，高二学生人数600人，高三学生人数500，从中抽取n人作为调查对象，得到了如图所示的这n人的频率分布直方图，这n人中有20人被学校界定为不健康生活方式者．
13．已知点P是抛物线y2=2x上的动点，F为抛物线的焦点，A（$\frac{7}{2}$，4），则|PA|+|PF|的最小值是（ ）
| A． | $\frac{7}{2}$ | B． | 5 | C． | $\frac{9}{2}$ | D． | 4 |