题目内容
设α为平面,m,n是两条不同的直线,下面命题中正确的是( )
| A、若m∥α,n∥α,则m∥n |
| B、若n⊥α,m⊥n,则m∥α |
| C、若m⊥n,m∥α,则n⊥α |
| D、若m⊥α,n∥α.则m⊥n |
考点:空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:根据空间直线和平面位置关系,结合平行或垂直的性质定理,即可得到结论.
解答:
解:A.平行于同一平面的两条直线可能平行,可能相交,可能是异面直线,故A错误.
B.若n⊥α,m⊥n,则m∥α或m?α,故B错误.
C.若m⊥n,m∥α,则n⊥α不一定成立,故C错误.
D.若m⊥α,n∥α.则m⊥n成立.
故选:D.
B.若n⊥α,m⊥n,则m∥α或m?α,故B错误.
C.若m⊥n,m∥α,则n⊥α不一定成立,故C错误.
D.若m⊥α,n∥α.则m⊥n成立.
故选:D.
点评:本题主要考查空间直线和平面位置关系的判断,要求熟练掌握平行或垂直的性质和判定定理.

练习册系列答案
相关题目
设i为虚数单位,则复数z=
在复平面内对应的点位于( )
| i3 |
| 1-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知点G是△ABC的重心,若A=
,
•
=3,则|
|的最小值为( )
| π |
| 3 |
| AB |
| AC |
| AG |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
已知x,y满足不等式组
,则目标函数z=2x+y的最大值为( )
|
| A、5 | B、6 | C、7 | D、8 |
已知a∈R,若
为实数,则a=( )
| 1+ai |
| 2-i |
| A、2 | ||
| B、-2 | ||
C、-
| ||
D、
|
 执行如图所示的程序框图,若输出b的值为15,则图中判断框内①处应填的数是( )
执行如图所示的程序框图,若输出b的值为15,则图中判断框内①处应填的数是( )| A、2 | B、3 | C、4 | D、5 |
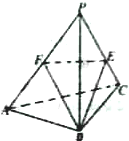 如图:已知正三棱锥P-ABC,侧棱PA,PB,PC的长为2,且∠APB=30°,E,F分别是侧棱PC,PA上的动点,则△BEF的周长的最小值为( )
如图:已知正三棱锥P-ABC,侧棱PA,PB,PC的长为2,且∠APB=30°,E,F分别是侧棱PC,PA上的动点,则△BEF的周长的最小值为( )A、8-4
| ||
| B、2 | ||
C、2
| ||
D、1+2
|

