题目内容
设i为虚数单位,则复数z=
在复平面内对应的点位于( )
| i3 |
| 1-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
考点:复数代数形式的乘除运算,复数的代数表示法及其几何意义
专题:数系的扩充和复数
分析:可先利用i2计算i3,再将分式的分子、分母分别乘以1+i,使分母“实数化”,除法问题通过乘法来解决,复数便化为代数形式,可知其对应的点所在象限.
解答:
解:由i2=-1,得i3=i2•i=-i,
从而z=
=
=
=
=
-
i,
则复数z在复平面内对应的点的坐标为(
,-
),此点位于第四象限,
故选D.
从而z=
| i3 |
| 1-i |
| -i |
| 1-i |
| -i(1+i) |
| (1-i)(1+i) |
| 1-i |
| 12+12 |
| 1 |
| 2 |
| 1 |
| 2 |
则复数z在复平面内对应的点的坐标为(
| 1 |
| 2 |
| 1 |
| 2 |
故选D.
点评:1.高考对复数的考查内容包括复数的概念与计算,要求不高,一般是容易题.
2.记住以下常用结论可以加快计算速度:
(1)i2=-1,i3=-i,i4=1;
(2)设z=a+bi(a,b∈R),则(a+bi)(a-bi)=a2+b2.
2.记住以下常用结论可以加快计算速度:
(1)i2=-1,i3=-i,i4=1;
(2)设z=a+bi(a,b∈R),则(a+bi)(a-bi)=a2+b2.

练习册系列答案
相关题目
已知动点P(x,y)满足
,动点Q(x,y)在曲线(x-1)2+y2=1上,则|PQ|的最大值与最小值的和为( )
|
A、
| ||||||
B、2
| ||||||
C、
| ||||||
D、3
|
设α为平面,m,n是两条不同的直线,下面命题中正确的是( )
| A、若m∥α,n∥α,则m∥n |
| B、若n⊥α,m⊥n,则m∥α |
| C、若m⊥n,m∥α,则n⊥α |
| D、若m⊥α,n∥α.则m⊥n |
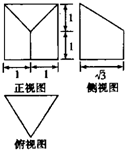
如图为一个几何体是三视图,则该几何体的表面积(不考虑接触点)为( )

A、6+
| ||
| B、32+π | ||
C、18+
| ||
D、18+2
|
在区间[0,π]内任取一个数x,则使sinx-cosx≤0的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|