题目内容
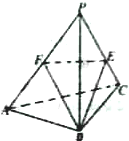如图：已知正三棱锥P-ABC，侧棱PA，PB，PC的长为2，且∠APB=30°，E，F分别是侧棱PC，PA上的动点，则△BEF的周长的最小值为（ ）A、8-4
| ||
| B、2 | ||
C、2
| ||
D、1+2
|
考点：棱锥的结构特征,空间中直线与直线之间的位置关系
专题：计算题,空间位置关系与距离
分析：利用棱锥的侧面展开图把△BEF的周长的最小值问题转化为两点之间的最短距离问题，解三角形可得答案．
解答：
解：正三棱锥的侧面展开图如图：
∵∠APB=30°，∴∠BPB1=90°，PB=2，
BB1=
=2
，
∴△BEF的周长的最小值为2
．
故选：C．
∵∠APB=30°，∴∠BPB1=90°，PB=2，
BB1=
| 4+4 |
| 2 |
∴△BEF的周长的最小值为2
| 2 |
故选：C．
点评：本题考查了利用棱锥的侧面展开图求最短距离问题，熟练掌握正棱锥的几何性质是解答问题的关键．
练习册系列答案
名校课堂系列答案
相关题目
设α为平面，m，n是两条不同的直线，下面命题中正确的是（ ）
| A、若m∥α，n∥α，则m∥n |
| B、若n⊥α，m⊥n，则m∥α |
| C、若m⊥n，m∥α，则n⊥α |
| D、若m⊥α，n∥α．则m⊥n |
已知集合A={-1，2，3}，B={y|y=x3，x∈A}，则A∩B=（ ）
| A、{0} | B、{1} |
| C、{-1} | D、{0，1} |
在区间[0，π]内任取一个数x，则使sinx-cosx≤0的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
对于任意给定的实数m，直线3x+y-m=0与双曲线
-
=1（a＞0，b＞0）最多有一个交点，则双曲线的离心率等于（ ）
| y2 |
| a2 |
| x2 |
| b2 |
A、
| ||||
B、
| ||||
| C、3 | ||||
D、2
|
设复数z1=1+i，z2=
-i，其中i为虚数单位，则
的实部为（ ）
| 3 |
| z1 |
| z2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设a1，a2，a3均为正数，λ1＜λ2＜λ3，则函数f（x）=
+
+
的两个零点分别位于区间（ ）
| a1 |
| x-λ1 |
| a2 |
| x-λ2 |
| a3 |
| x-λ3 |
| A、（-∞，λ1）∪（λ1，λ2）内 |
| B、（λ1，λ2）∪（λ2，λ3）内 |
| C、（λ2，λ3）∪（λ3，+∞）内 |
| D、（-∞，λ1）∪（λ3，+∞）内 |