题目内容
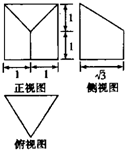
某几何体的三视图及部分数据如图所示,则此几何体的表面积是 .


考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由已知中的三视图,可得该几何体是由一个正方体加一个圆柱,所得的组合体,进而可得答案.
解答:
解:由已知中的三视图,可得该几何体是由一个正方体加一个圆柱,所得的组合体,
其中圆柱的直径为2,高为4,
∴S圆柱侧=2×π×4=8π,
正方体的棱长为4,
∴S正方体=6×4×4=96,
故组合体的表面积S=8π+96.
故答案为:8π+96
其中圆柱的直径为2,高为4,
∴S圆柱侧=2×π×4=8π,
正方体的棱长为4,
∴S正方体=6×4×4=96,
故组合体的表面积S=8π+96.
故答案为:8π+96
点评:本题考查的知识点是由三视图求表面积,其中分析出几何体的形状是解答的关键.

练习册系列答案
相关题目
设α为平面,m,n是两条不同的直线,下面命题中正确的是( )
| A、若m∥α,n∥α,则m∥n |
| B、若n⊥α,m⊥n,则m∥α |
| C、若m⊥n,m∥α,则n⊥α |
| D、若m⊥α,n∥α.则m⊥n |
已知集合A={-1,2,3},B={y|y=x3,x∈A},则A∩B=( )
| A、{0} | B、{1} |
| C、{-1} | D、{0,1} |