题目内容

已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点分别是F1，F2，右顶点为A，上顶点为B，若椭圆C的中点到直线AB的距离为
6
6
|F1F2|，则椭圆C的离心率e=（　　）
A、
2
2
B、
3
2
C、
5
2
D、
3
3
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：求出直线AB的方程，通过椭圆的中心到直线的距离列出方程，得到a、b、c的关系式，然后求解椭圆的离心率．
解答： 解：设椭圆C的焦距为2c（c＜a），
由于直线AB的方程为ax+by-ab=0，
所以
ab
a2+b2
=
6
3
c，
因b2=a2-c2，所以3a4-7a2c2+2c4=0，
解得a2=2c2或3a2=c2（舍），
所以e=
2
2
．
故选：A．
点评：本题考查椭圆的简单性质，椭圆的离心率的求法，点到直线的距离公式的应用，考查计算能力．
练习册系列答案
相关题目
某个体服装店经营某种服装，一周内获纯利润y（元）与该周每天销售这种服装的件数x之间的一组数据如下：
x3456789
y66697381899091
已知
7
i=1
x
2
i
=280，
7
i=1
y
2
i
=45309，
7
i=1
xiyi=3487，此时r0.05=0.754
（1）求
.
x
，
.
y
；
（2）判断一周内获纯利润y与该周每天销售件数x之间是否线性相关，如果线性相关，求出线性回归方程．
已知a b c∈R+，a+
2
b+
3
c=2
3
，记a2+b2+c2的最小值为m．
（Ⅰ）求实数rn；
（Ⅱ）若关于x的不等式|x-3|≥m和x2+px+q≥0的解集相同，求p的值．
设f（x）=ax3+bx2+cx+d（a≠0）．已知五个方程的相异实根个数如下表所述﹕
f（x）-20=01f（x）+10=01
f（x）-10=03f（x）+20=01
f（x）=03
α为关于f（x）的极大值﹐下列选项中正确的是（　　）
A、0＜α＜10
B、10＜α＜20
C、-10＜α＜0
D、-20＜α＜-10
平面向量
a
，
b
中，|
a
|≠0，
b
=t
a
（t∈R）．对于使命题“?t＞1，|
c
-
b
|≥|
c
-
a
|”为真的非零向量
c
，给出下列命题：
①?t＞1，（
c
-
a
）•（ 
b
-
a
）≤0；    ②?t＞1，（ 
c
-
a
）•（
b
-
a
）＞0；
③?t∈R，（
c
-
a
）•（ 
c
-
b
）＜0；   ④?t∈R，（
c
-
a
）•（
c
-
b
）＜0．
则以上四个命题中的真命题是（　　）
A、①④B、②③
C、①②④D、①③④
若数列{an}对任意的正整数n和常数λ（λ∈N），等式an+λ2=an×an+2λ都成立，则称数列{an}为“λ阶梯等比数列”，
an+λ
an
的值称为“阶梯比”，若数列{an}是3阶梯等比数列且a1=1，a4=2．则a10=
 
．
如图，在平面直角坐标系xOy中，将直线y=
x
2
与直线x=1及x轴所围成的图形旋转一周得到一个圆锥，圆锥的体积V圆锥=
∫
1
0
π（
x
2
）2dx=
π
12
x3|
0
1
=
π
12
．
据此类推：将曲线y=x2与直线y=4所围成的图形绕y轴旋转一周得到一个旋转体，该旋转体的体积V=
 
．
定义在实数集R上的函数f（x），对任意x，y∈R，有f（x-y）+f（x+y）=2f（x）f（y），且f（0）≠0．
求证：f（x）是偶函数．
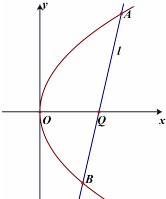已知抛物线G：y2=2px（p＞0）的焦点到准线的距离为2，过点Q（a，0）（a＞0）的直线l交抛物线G于A，B两点（如图所示）． 
（Ⅰ）求抛物线G的方程；
（Ⅱ）有人发现，当点Q为抛物线的焦点时，
1
|QA|
+
1
|QB|
的值与直线l的方向无关．受其启发，你能否找到一个点Q，使得
1
|QA|2
+
1
|QB|2
的值也与直线l的方向无关．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网