Question

在平面直角坐标系中，不等式

x+y-4≤0 x-y+a≥0 x≥0 y≥0

（a为常数且0＜a＜4）表示的平面区域的面积为7，则3x-2y的最小值为

 

．

Answer 1

考点：简单线性规划

专题：不等式的解法及应用

分析：作出不等式对应的平面区域，根据平面区域面积，求出a的值，利用线性规划的知识，通过平移即可求z的最小值．

解答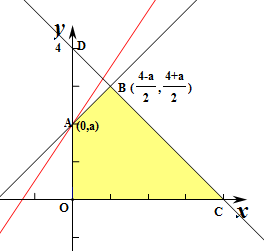： 解：作出不等式组对应的平面区域如图：（阴影部分）
则A（0，a），C（4，0），B（

4-a

2

，

4+a

2

），D（

4-a

2

，0）．
则阴影部分的面积S=S_△OBC-S_△ABD=

1

2

×4×4-

1

2

（4-a）×

4-a

2

=7，
即（4-a）²=4，
解得a=2，
设z=3x-2y得y=

3

2

x-

z

2

，
平移直线y=

3

2

x-

z

2

，
由图象可知当直线y=

3

2

x-

z

2

经过点A（0，2）时，直线y=

3

2

x-

z

2

的截距最大，
此时z最小．即z=3x-2y得z=0-2×2=-4．
即z的最小值为-4．
故答案为：-4．

点评：本题主要考查线性规划的应用，先根据图象的面积求出a的值，是解决本题的关键，利用数形结合是解决线性规划问题中的基本方法．