题目内容
对于定义域内的任意实数x,函数f(x)=
的值恒为正数,则实数a的取值范围是 .
| x2+(a-1)x-2a+2 |
| 2x2+ax-2a |
考点:函数恒成立问题
专题:函数的性质及应用
分析:题目给出的函数是分式函数,且分子分母均为二次三项式,对应的函数均开口向上,所以分分子分母对应的方程同解和不同解讨论,同解时利用系数相等求a的值,不同解时,若a≠0,则需分子分母对应的方程均无解,a=0时,在定义域内函数值恒大于0.
解答:
解:给出的函数分子分母都是二次三项式,对应的图象都是开口向上的抛物线,若分子分母对应的方程是同解方程,
则
,解得a=2.
此时函数的值为f(x)=
>0.
若分子分母对应的方程不是同解方程,要保证对于定义域内的任意实数x,函数值均为正,
则需要分子分母的判别式均小于0,
即
,
解得-7<a<0.
∴a的范围是-7<a<0.
当a=0时,函数化为f(x)=
,函数定义域为{x|x≠0},分母恒大于0,分子的判别式小于0,
分子恒大于0,函数值恒正.
综上,对于定义域内的任意实数x,函数值均为正,则实数a的取值范围是-7<a≤0或a=2.
故答案为:-7<a≤0或a=2.
则
|
此时函数的值为f(x)=
| 1 |
| 2 |
若分子分母对应的方程不是同解方程,要保证对于定义域内的任意实数x,函数值均为正,
则需要分子分母的判别式均小于0,
即
|
解得-7<a<0.
∴a的范围是-7<a<0.
当a=0时,函数化为f(x)=
| x2-x+2 |
| 2x2 |
分子恒大于0,函数值恒正.
综上,对于定义域内的任意实数x,函数值均为正,则实数a的取值范围是-7<a≤0或a=2.
故答案为:-7<a≤0或a=2.
点评:本题考查恒成立问题,考查了利用函数值的范围求解参数的取值范围,解答此题的关键是由函数值恒为正得到分子分母的取值情况,属中档题.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
按如图所示程序框,最后输出i的结果是( )

| A、5 | B、6 | C、7 | D、8 |
若向量
=(6,x)(x∈R)则“x=8”是“|
|=10”的( )
| a |
| a |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
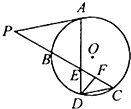 如图,A是⊙O上的点,PC与⊙O相交于B、C两点,点D在⊙O上,CD∥AP,AD与BC交于E,F为CE上的点,若∠EDF=∠P,BE=8,EF=4,FC=5,则PB=
如图,A是⊙O上的点,PC与⊙O相交于B、C两点,点D在⊙O上,CD∥AP,AD与BC交于E,F为CE上的点,若∠EDF=∠P,BE=8,EF=4,FC=5,则PB=