题目内容
已知函数f(x)=(
)|a-2x|的图象关于直线x=1对称,则a的值为 .
| 1 |
| 3 |
考点:指数函数的图像变换
专题:函数的性质及应用
分析:设t=|a-2x|,则根据函数的对称性建立条件关系即可得到结论.
解答:
解:设t=|a-2x|,则f(x)=(
)|a-2x|的图象关于直线x=1对称,
则等价为t=|a-2x|关于x=1对称,
即当x=1时,t=|a-2|=0,
解得a=2,
故答案为:2
| 1 |
| 3 |
则等价为t=|a-2x|关于x=1对称,
即当x=1时,t=|a-2|=0,
解得a=2,
故答案为:2
点评:本题主要考查函数对称性的求解,利用换元法转化为绝对值的对称性是解决本题的关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
已知四棱锥P-ABCD的三视图如图所示,则此四棱锥的四个侧面的面积中最大的是( )


| A、3 | ||||
B、
| ||||
C、3
| ||||
D、
|
按如图所示程序框,最后输出i的结果是( )

| A、5 | B、6 | C、7 | D、8 |
已知偶函数f(x)的定义域为R,对任意x∈R,有f(x+2)=f(x),当x∈[0,1]时,f(x)=-x+1.则函数g(x)=log6|x|-f(x)的零点的个数是( )
| A、6个 | B、8个 |
| C、10个 | D、12个 |
已知圆F的圆心为双曲线
-
=1的右焦点,且与该双曲线的渐近线相切,则圆F的方程为( )
| x2 |
| 5 |
| y2 |
| 4 |
| A、(x+3)2+y2=4 |
| B、(x+3)2+y2=2 |
| C、(x-3)2+y2=4 |
| D、(x-3)2+y2=2 |

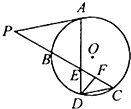 如图,A是⊙O上的点,PC与⊙O相交于B、C两点,点D在⊙O上,CD∥AP,AD与BC交于E,F为CE上的点,若∠EDF=∠P,BE=8,EF=4,FC=5,则PB=
如图,A是⊙O上的点,PC与⊙O相交于B、C两点,点D在⊙O上,CD∥AP,AD与BC交于E,F为CE上的点,若∠EDF=∠P,BE=8,EF=4,FC=5,则PB=