题目内容
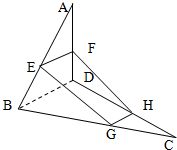如图，空间四边形ABCD中，E，F分别是AB，AD边上的中点，G，H分别是BC，CD边上的点，且| CG |
| GB |
| CH |
| HD |
| 1 |
| 2 |
考点：空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：由已知条件推导出EF∥HG，且EF≠HG，由此能证明四边形GHFE是梯形．
解答：
证明：∵空间四边形ABCD中，E，F分别是AB，AD边上的中点，
∴EF∥BD，且EF=
BD，
∵G，H分别是BC，CD边上的点，且
=
=
，
∴HG∥BD，且HG=
BD，
∴EF∥HG，且EF≠HG，
∴四边形GHFE是梯形．
∴EF∥BD，且EF=
| 1 |
| 2 |
∵G，H分别是BC，CD边上的点，且
| CG |
| GB |
| CH |
| HD |
| 1 |
| 2 |
∴HG∥BD，且HG=
| 1 |
| 3 |
∴EF∥HG，且EF≠HG，
∴四边形GHFE是梯形．
点评：本题考查四边形是梯形的证明，解题时要注意三角形中位线定理和平行线等分线段成比例的灵活运用．
练习册系列答案
相关题目
如图，MA⊥平面ABCD，四边形ABCD为菱形，四边形ADNM为平行四边形，点E为AB中点．
如图，已知圆G：x2+y2-2x-
如图，在三棱锥S-ABC中，SC⊥平面ABC，M、N分别是SB和SC的中点，设MN=AC=1，∠ACB=90°，直线AM与直线SC所成的角为60°