题目内容
 如图所示,在直四棱柱ABCD-A1B1C1D1中,底面ABCD是矩形,AB=1,BC=
如图所示,在直四棱柱ABCD-A1B1C1D1中,底面ABCD是矩形,AB=1,BC=| 2 |
(1)求四面体A-A1ED的体积;
(2)求异面直线AE与B1D所成角的大小.(结果用反三角函数表示)
考点:异面直线及其所成的角,棱柱、棱锥、棱台的体积
专题:空间角
分析:(1)由已知条件求出△A1ED的面积,再由VA-A1ED=VE-A1AD,利用等积法能求出四面体A-A1KD的体积.
(2)取CC1中点F,连结DF,B1F.因为DF∥AE,所以DF与B1D所成的角的大小等于异面直线AE与B1D所成的角的大小.由此能求出异面直线AE与B1D所成的角的大小.
(2)取CC1中点F,连结DF,B1F.因为DF∥AE,所以DF与B1D所成的角的大小等于异面直线AE与B1D所成的角的大小.由此能求出异面直线AE与B1D所成的角的大小.
解答:
(本题满分12分)本题共有2小题,第1小题满分(6分),第2小题满分(6分).
解:(1)因为在直四棱柱ABCD-A1B1C1D1中,
底面ABCD是矩形,AB=1,BC=
,AA1=2,E是侧棱BB1的中点,
所以S△A1ED=
×2×
=
,
所以VA-A1ED=VE-A1AD=
S△A1ED•AB=
.
(2)取CC1中点F,连结DF,B1F.
因为DF∥AE,所以DF与B1D所成的角的大小等于异面直线AE与B1D所成的角的大小.
在△B1DF中,B1D=
,DF=
,B1F=
,
所以cos∠B1DF=
=
,
所以异面直线AE与B1D所成的角为arccos
.
解:(1)因为在直四棱柱ABCD-A1B1C1D1中,
底面ABCD是矩形,AB=1,BC=
| 2 |
所以S△A1ED=
| 1 |
| 2 |
| 2 |
| 2 |
所以VA-A1ED=VE-A1AD=
| 1 |
| 3 |
| ||
| 3 |
(2)取CC1中点F,连结DF,B1F.
因为DF∥AE,所以DF与B1D所成的角的大小等于异面直线AE与B1D所成的角的大小.
在△B1DF中,B1D=
| 7 |
| 2 |
| 3 |
所以cos∠B1DF=
| DF2+DB12-B1F2 |
| 2DF•DB1 |
3
| ||
| 14 |
所以异面直线AE与B1D所成的角为arccos
3
| ||
| 14 |
点评:本题考查四面体的体积的求法,考查异面直线所成角的求法,是中档题,解题时要注意空间思维能力的培养.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 A,B是焦点为F的抛物线y2=4x上的两动点,线段AB的中点M在直线x=t(t>0)上.
A,B是焦点为F的抛物线y2=4x上的两动点,线段AB的中点M在直线x=t(t>0)上.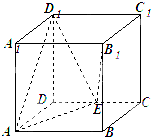 正方体ABCD-A1B1C1D1中,点E在棱CD上.
正方体ABCD-A1B1C1D1中,点E在棱CD上. 已知函数f(x)=3sin(2x-
已知函数f(x)=3sin(2x- 如图,已知平面四边形ABCP中,D为PA的中点,PA⊥AB,CD∥AB,且PA=CD=2AB=4.将此平面四边形ABCP沿CD折成直二面角P-DC-B,连接PA、PB,设PB中点为E.
如图,已知平面四边形ABCP中,D为PA的中点,PA⊥AB,CD∥AB,且PA=CD=2AB=4.将此平面四边形ABCP沿CD折成直二面角P-DC-B,连接PA、PB,设PB中点为E.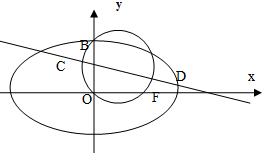 如图,已知圆G:x2+y2-2x-
如图,已知圆G:x2+y2-2x-