题目内容
如图1,边长为2的正方形ABCD中,E是AB边的中点,F是BC边上的一点,对角线AC分别交DE、DF于M、N两点,将△DAE及△DCF折起,使A、C重合于G点,构成如图2所示的几何体.
(Ⅰ)求证:GD⊥EF;
(Ⅱ)若EF∥平面GMN,求三棱锥G-EFD的体积VG-EFD.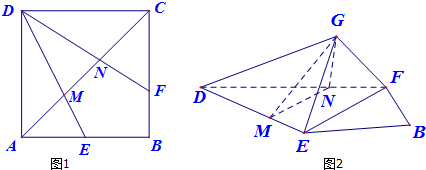
(Ⅰ)求证:GD⊥EF;
(Ⅱ)若EF∥平面GMN,求三棱锥G-EFD的体积VG-EFD.

考点:棱柱、棱锥、棱台的体积,空间中直线与直线之间的位置关系
专题:计算题,证明题,空间位置关系与距离
分析:(Ⅰ)注意到DA⊥AE,DC⊥CF,则折起后DG⊥GE,DG⊥GF,从而证明DG⊥平面EFG,从而得证;
(Ⅱ)由EF∥平面GMN可得EF∥MN,从而可知EF是△ABC的中位线,从而求三棱锥G-EFD的体积VG-EFD.
(Ⅱ)由EF∥平面GMN可得EF∥MN,从而可知EF是△ABC的中位线,从而求三棱锥G-EFD的体积VG-EFD.
解答:
解:(Ⅰ)证明:∵DA⊥AE,DC⊥CF,
∴DG⊥GE,DG⊥GF,
又∵GE∩GF=G,
∴DG⊥平面EFG,
∴GD⊥EF.
(Ⅱ)∵EF∥平面GMN,
∴EF∥MN,
又∵E是AB边的中点,
∴F是BC边上的中点,
∴GE⊥GF,
∴VG-EFD=VD-GEF=
×
×1×1×2=
.
∴DG⊥GE,DG⊥GF,
又∵GE∩GF=G,
∴DG⊥平面EFG,
∴GD⊥EF.
(Ⅱ)∵EF∥平面GMN,
∴EF∥MN,
又∵E是AB边的中点,
∴F是BC边上的中点,
∴GE⊥GF,
∴VG-EFD=VD-GEF=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
点评:本题考查了线面垂直的判定与应用,同时考查了体积的求法,属于中档题.

练习册系列答案
相关题目
若sina•
-cosa•
=-1,且a≠
﹙k∈z﹚,则a所在的象限是( )
| (sin2a) |
| (cos2a) |
| kπ |
| 2 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
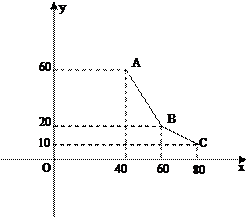 小张经营某一消费品专卖店,已知该消费品的进价为每件40元,该店每月销售量y(百件)与销售单价x(元/件)之间的关系用如图的一折线表示,职工每人每月工资为1000元,该店还应交付的其它费用为每月10000元.
小张经营某一消费品专卖店,已知该消费品的进价为每件40元,该店每月销售量y(百件)与销售单价x(元/件)之间的关系用如图的一折线表示,职工每人每月工资为1000元,该店还应交付的其它费用为每月10000元.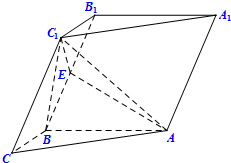 如图,在三棱柱ABC-A1B1C1中,已知AB⊥BB1C1C,BC=1,AB=BB1=2,∠BCC1=
如图,在三棱柱ABC-A1B1C1中,已知AB⊥BB1C1C,BC=1,AB=BB1=2,∠BCC1= 已知函数f(x)是定义在R上的偶函数,已知x≥0时,f(x)=x2-2x.
已知函数f(x)是定义在R上的偶函数,已知x≥0时,f(x)=x2-2x.