题目内容
已知|
|=
，|
|=1，
与
的夹角为135°．
（1）求（
+
）•（2
-
）的值；
（2）若k为实数，求|
+k
|的最小值．
| a |
| 2 |
| b |
| a |
| b |
（1）求（
| a |
| b |
| a |
| b |
（2）若k为实数，求|
| a |
| b |
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：（1）利用平面向量数量积的运算，即可求（
+
）•（2
-
）的值；
（2）先求模，再利用配方法，即可求|
+k
|的最小值．
| a |
| b |
| a |
| b |
（2）先求模，再利用配方法，即可求|
| a |
| b |
解答：
解：（1）因为|
|=
，|
|=1，
与
的夹角为135°，
所以(
+
)•(2
-
)=2
2-
2+
•
=4-1+
×1×(-
)=2． …（6分）
（2）|
+k
|2=
2+k2
2+2k
•
=k2-2k+2=（k-1）2+1．…（10分）
当k=1时，|
+k
|2的最小值为1，…（12分）
即|
+k
|的最小值为1． …（14分）
| a |
| 2 |
| b |
| a |
| b |
所以(
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| 2 |
| ||
| 2 |
（2）|
| a |
| b |
| a |
| b |
| a |
| b |
当k=1时，|
| a |
| b |
即|
| a |
| b |
点评：本题考查平面向量数量积的运算，考查配方法的运用，属于中档题．
练习册系列答案
相关题目
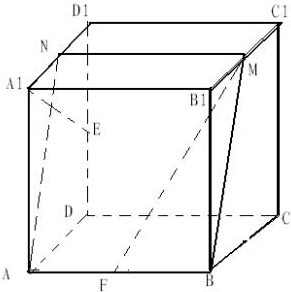如图，在正方体ABCD-A1B1C1D1中，M，N，E，F，F分别是棱B1C1，A1D1，D1D，AB的中点．