Question

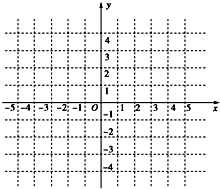已知函数f（x）是定义在R上的偶函数，已知x≥0时，f（x）=x²-2x．
（1）画出偶函数f（x）的图象的草图，并求函数f（x）的单调递增区间；
（2）当直线y=k（k∈R）与函数y=f（x）恰有4个交点时，求k的取值范围．

Answer 1

考点：二次函数的性质,函数奇偶性的性质

专题：函数的性质及应用

分析：（1）根据已知条件画出函数f（x）的图象，根据图象即可得到f（x）的单调递增区间；
（2）通过图象即可得到k的取值范围．

解答： 解：（1）画出f（x）的图象如下图：

由图象知，函数f（x）单调递增区间为[-1，0]，[1，+∞）；
（2）由图象可知，当-1＜k＜0时，直线与函数y=f（x）的图象的交点个数为4；
∴k的取值范围为（-1，0）．

点评：考查偶函数的概念，偶函数图象的特点，以及根据图象求函数的单调区间，以及根据图象得出使得y=k和f（x）图象有四个交点时k的取值范围．