题目内容
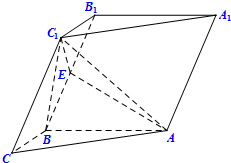 如图,在三棱柱ABC-A1B1C1中,已知AB⊥BB1C1C,BC=1,AB=BB1=2,∠BCC1=
如图,在三棱柱ABC-A1B1C1中,已知AB⊥BB1C1C,BC=1,AB=BB1=2,∠BCC1=| π |
| 3 |
(Ⅰ)求证:C1B⊥平面ABC;
(Ⅱ)P是线段BB1上的动点,当平面C1AP⊥平面AA1B1B时,求线段B1P的长;
(Ⅲ)若E为BB1的中点,求二面角C1-AE-A1平面角的余弦值.
考点:与二面角有关的立体几何综合题,直线与平面垂直的判定
专题:计算题,空间位置关系与距离,空间角
分析:(Ⅰ)运用线面垂直的判定和性质定理,即可得证;
(Ⅱ)由面面垂直的判定定理,可得面ABB1A1⊥面BB1C1C过C1作C1P⊥BB1于P,则C1P⊥面AA1B1B,在直角三角形BB1C1中,即可解得B1P;
(Ⅲ)运用线面垂直的判断和性质,过P作PH⊥AE,交AE所在直线于点H,则有∠C1HP为二面角C1-AE-A1平面角.再在三角形C1HP中,即可得到平面角的余弦值.
(Ⅱ)由面面垂直的判定定理,可得面ABB1A1⊥面BB1C1C过C1作C1P⊥BB1于P,则C1P⊥面AA1B1B,在直角三角形BB1C1中,即可解得B1P;
(Ⅲ)运用线面垂直的判断和性质,过P作PH⊥AE,交AE所在直线于点H,则有∠C1HP为二面角C1-AE-A1平面角.再在三角形C1HP中,即可得到平面角的余弦值.
解答:
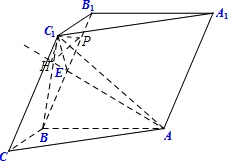 (Ⅰ)证明:AB⊥侧面BB1C1C,得AB⊥C1B,
(Ⅰ)证明:AB⊥侧面BB1C1C,得AB⊥C1B,
由BC=1,CC1=BB1=2,∠BCC1=
,
知∠C1BC=90°,即C1B⊥CB,
又CB∩BA=A,
故C1B⊥平面ABC;
(Ⅱ)解:由已知AB⊥侧面BB1C1C,
知面ABB1A1⊥面BB1C1C,
过C1作C1P⊥BB1于P,
则C1P⊥面AA1B1B,
因C1P?面C1AP,
故平面C1AP⊥平面AA1B1B,
在直角三角形BB1C1中,
B1P=B1C1cos60°=
;
(Ⅲ)解:由(Ⅱ)知C1P⊥面AA1B1B,
过P作PH⊥AE,交AE所在直线于点H,
则AE⊥平面C1HP,即有AE⊥C1H,
∠C1HP为二面角C1-AE-A1平面角.
由三角形相似求得:PH=
,又C1P=
,
∴tan∠C1HP=
=
/
=
,
故cos∠C1HP=
.
 (Ⅰ)证明:AB⊥侧面BB1C1C,得AB⊥C1B,
(Ⅰ)证明:AB⊥侧面BB1C1C,得AB⊥C1B,由BC=1,CC1=BB1=2,∠BCC1=
| π |
| 3 |
知∠C1BC=90°,即C1B⊥CB,
又CB∩BA=A,
故C1B⊥平面ABC;
(Ⅱ)解:由已知AB⊥侧面BB1C1C,
知面ABB1A1⊥面BB1C1C,
过C1作C1P⊥BB1于P,
则C1P⊥面AA1B1B,
因C1P?面C1AP,
故平面C1AP⊥平面AA1B1B,
在直角三角形BB1C1中,
B1P=B1C1cos60°=
| 1 |
| 2 |
(Ⅲ)解:由(Ⅱ)知C1P⊥面AA1B1B,
过P作PH⊥AE,交AE所在直线于点H,
则AE⊥平面C1HP,即有AE⊥C1H,
∠C1HP为二面角C1-AE-A1平面角.
由三角形相似求得:PH=
| ||
| 5 |
| ||
| 2 |
∴tan∠C1HP=
| C1P |
| PH |
| ||
| 2 |
| ||
| 5 |
| ||
| 2 |
故cos∠C1HP=
2
| ||
| 19 |
点评:本题考查空间直线与平面的位置关系:垂直,考查线面垂直的判断和性质,以及面面垂直的判定和性质,考查空间的二面角的求法,考查运算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
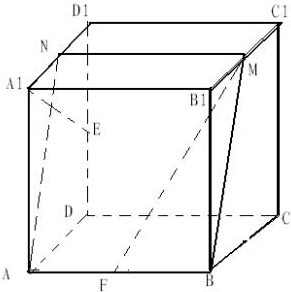 如图,在正方体ABCD-A1B1C1D1中,M,N,E,F,F分别是棱B1C1,A1D1,D1D,AB的中点.
如图,在正方体ABCD-A1B1C1D1中,M,N,E,F,F分别是棱B1C1,A1D1,D1D,AB的中点.