题目内容
若sina•
-cosa•
=-1，且a≠
﹙k∈z﹚，则a所在的象限是（ ）
| (sin2a) |
| (cos2a) |
| kπ |
| 2 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：化简等式，得出结论
，结合题意，判断a是第几象限角．
|
解答：
解：∵sina•
-cosa•
=-1，
∴sina•|sina|-cosa•|cosa|=-1，
即-sina•sina-cosa•cosa=-1，
∴
；
又∵a≠
﹙k∈z﹚，
∴a在第四象限．
故选：D．
| (sin2a) |
| (cos2a) |
∴sina•|sina|-cosa•|cosa|=-1，
即-sina•sina-cosa•cosa=-1，
∴
|
又∵a≠
| kπ |
| 2 |
∴a在第四象限．
故选：D．
点评：本题考查了三角函数的符号判断问题，解题时应熟记三角符号的判断问题，是基础题．
练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
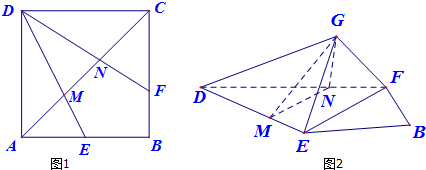
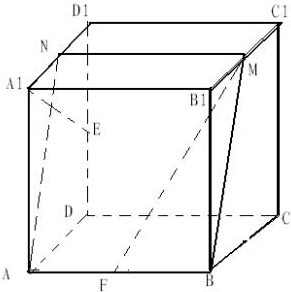如图，在正方体ABCD-A1B1C1D1中，M，N，E，F，F分别是棱B1C1，A1D1，D1D，AB的中点．