题目内容
在数列{an},{bn}中a1=2,an=an-1+2n,且an,bn,an+1成等差数列.
(1)求{an},{bn}的通项公式;
(2)证明:
+
+…+
<
.
(1)求{an},{bn}的通项公式;
(2)证明:
| 1 |
| a1+b1 |
| 1 |
| a2+b2 |
| 1 |
| an+bn |
| 5 |
| 12 |
考点:数列与不等式的综合
专题:计算题,证明题,等差数列与等比数列,不等式的解法及应用
分析:(1)运用an=a1+(a2-a1)+(a3-a2)+…+(an-an-1),即可得到{an}的通项公式,再由等差数列的中项性质,即可求得{bn}的通项公式;
(2)运用放缩法和裂项相消法,由于n>1时,
<
=
•
=
(
-
),从第二项起,放缩求和即可得证.
(2)运用放缩法和裂项相消法,由于n>1时,
| 1 |
| 2n2+3n+1 |
| 1 |
| 2n2+2n |
| 1 |
| 2 |
| 1 |
| n(n+1) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+1 |
解答:
(1)解:a1=2,an=an-1+2n,(n>1,n∈N),
则an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)
=2+2×2+2×3+…+2n
=2+
(4+2n)(n-1)=n2+n,
由an,bn,an+1成等差数列,则2bn=an+an+1
=n2+n+(1+n)2+n+1=2n2+4n+2,
则bn=n2+2n+1,
故an=n2+n,bn=n2+2n+1;
(2)证明:要证
+
+…+
<
,
即证
+
+…+
<
由于n=1时,
<
成立,即证n>1时成立即可.
由于n>1时,
<
=
•
=
(
-
),
则有
+…+
<
(
-
+
-
+…+
-
)
=
-
,
即有
+
+…+
<
+
-
<
+
=
.
则原不等式成立.
则an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)
=2+2×2+2×3+…+2n
=2+
| 1 |
| 2 |
由an,bn,an+1成等差数列,则2bn=an+an+1
=n2+n+(1+n)2+n+1=2n2+4n+2,
则bn=n2+2n+1,
故an=n2+n,bn=n2+2n+1;
(2)证明:要证
| 1 |
| a1+b1 |
| 1 |
| a2+b2 |
| 1 |
| an+bn |
| 5 |
| 12 |
即证
| 1 |
| 2+4 |
| 1 |
| 6+9 |
| 1 |
| 2n2+3n+1 |
| 5 |
| 12 |
由于n=1时,
| 1 |
| 6 |
| 5 |
| 12 |
由于n>1时,
| 1 |
| 2n2+3n+1 |
| 1 |
| 2n2+2n |
| 1 |
| 2 |
| 1 |
| n(n+1) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+1 |
则有
| 1 |
| 6+9 |
| 1 |
| 2n2+3n+1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
=
| 1 |
| 4 |
| 1 |
| 2(n+1) |
即有
| 1 |
| 2+4 |
| 1 |
| 6+9 |
| 1 |
| 2n2+3n+1 |
| 1 |
| 6 |
| 1 |
| 4 |
| 1 |
| 2(n+1) |
| 1 |
| 6 |
| 1 |
| 4 |
| 5 |
| 12 |
则原不等式成立.
点评:本题考查等差数列的通项和性质,以及求和,考查累加法和裂项相消求和的方法,考查运算能力,属于中档题和易错题.

练习册系列答案
相关题目
已知△ABC面积为1,点P满足
=
+
,在△ABC内任取M,那么落入△BPC内的概率为( )
| AP |
| 1 |
| 5 |
| AB |
| 1 |
| 4 |
| AC |
A、
| ||
B、
| ||
C、
| ||
D、
|
在平面直角坐标系xOy中,已知
、
是互相垂直的两个单位向量,点Q满足
=3
+4
.曲线C={P|
=2
cosθ+2
sinθ,0≤θ≤2π},区域Ω={P|0<r≤|
|≤R,r<R}.若C∩Ω=C,则( )
| a |
| b |
| OQ |
| a |
| b |
| OP |
| a |
| b |
| PQ |
| A、0<r≤3且R≥7 |
| B、0<r≤3≤R≤7 |
| C、0<r≤5<R<7 |
| D、5≤r<7≤R |
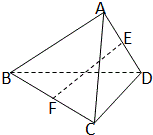 如图,在四面体ABCD中,E、F分别是AD、BC中,AB=CD=2,EF=
如图,在四面体ABCD中,E、F分别是AD、BC中,AB=CD=2,EF=