题目内容
 某海岛上有一座海拔1千米的山,山顶上有一观察站P(P在海平面上的射影点为A),测得一游艇在海岛南偏西30°,俯角为45°的B处,该游艇准备前往海岛正东方向,俯角为45°的旅游景点C处,如图所示.
某海岛上有一座海拔1千米的山,山顶上有一观察站P(P在海平面上的射影点为A),测得一游艇在海岛南偏西30°,俯角为45°的B处,该游艇准备前往海岛正东方向,俯角为45°的旅游景点C处,如图所示.(Ⅰ)设游艇从B处直线航行到C处时,距离观察站P最近的点为D处.
(i)求证:BC⊥平面PAD;(ii)计算B、D两点间的距离.
(Ⅱ)海水退潮后,在(Ⅰ)中的点D处周围0.25千米内有暗礁,航道变窄,为了有序参观景点,要求游艇从B处直线航行到A的正东方向某点E处后,再沿正东方向继续驶向C处.为使游艇不会触礁,试求AE的最大值.
考点:函数与方程的综合运用,解三角形的实际应用
专题:解三角形,空间位置关系与距离
分析:(Ⅰ)(i)连结PD,AD,由已知结合线面垂直的性质,可得PD⊥BC,PA⊥BC,再由线面垂直的判定定理,可得BC⊥平面PAD;
(ii)解直角三角形,求出AB=1,AC=1,且∠BAC=120°,则∠ABC=∠ACB=30°,结合BC⊥AD,可得D为BC的中点,且BD=
;
(Ⅱ)由题意过点B作圆D的切线,交AC于E,切点为G,则AE取得最大值,设AE=x,连结DG,则DG⊥BE,结合余弦定理构造方程,可得AE的最大值.
(ii)解直角三角形,求出AB=1,AC=1,且∠BAC=120°,则∠ABC=∠ACB=30°,结合BC⊥AD,可得D为BC的中点,且BD=
| ||
| 2 |
(Ⅱ)由题意过点B作圆D的切线,交AC于E,切点为G,则AE取得最大值,设AE=x,连结DG,则DG⊥BE,结合余弦定理构造方程,可得AE的最大值.
解答:
解:(Ⅰ) (i)连结PD,AD,
(i)连结PD,AD,
∵游艇距离观察站P最近的点为D处,
∴PD⊥BC,
又由题意得:PA⊥平面ABC,BC?平面ABC,
∴PA⊥BC,
又∵PD∩PA=P,PA,PD?平面PAD,
∴BC⊥平面PAD;
(ii)∵PA⊥平面ABC,AB?平面ABC,
∴PA⊥AB,
又∵∠PBA=45°,PA=1,
∴AB=1,
同理AC=1,且∠BAC=120°,
∴∠ABC=∠ACB=30°,
又BC⊥AD,
∴D为BC的中点,且BD=
;

(Ⅱ)由题意过点B作圆D的切线,交AC于E,切点为G,
则AE取得最大值,
设AE=x,则CE=1-x,过点E作EF⊥BC于F,
则EF=
(1-x),
连结DG,则DG⊥BE,
∴Rt△BGD∽Rt△BFE,
∴DG:EF=BD:BE,
∴BE=
(1-x),
在△ABE中,BE2=AB2+AE2-
AB•AE•cos∠BAC,
即3(1-x)2=1+x2+x,
解得:x=
,或x=
,
又由0<x<1,
∴x=
,
即AE的最大值为
.
 (i)连结PD,AD,
(i)连结PD,AD,∵游艇距离观察站P最近的点为D处,
∴PD⊥BC,
又由题意得:PA⊥平面ABC,BC?平面ABC,
∴PA⊥BC,
又∵PD∩PA=P,PA,PD?平面PAD,
∴BC⊥平面PAD;
(ii)∵PA⊥平面ABC,AB?平面ABC,
∴PA⊥AB,
又∵∠PBA=45°,PA=1,
∴AB=1,
同理AC=1,且∠BAC=120°,
∴∠ABC=∠ACB=30°,
又BC⊥AD,
∴D为BC的中点,且BD=
| ||
| 2 |

(Ⅱ)由题意过点B作圆D的切线,交AC于E,切点为G,
则AE取得最大值,
设AE=x,则CE=1-x,过点E作EF⊥BC于F,
则EF=
| 1 |
| 2 |
连结DG,则DG⊥BE,
∴Rt△BGD∽Rt△BFE,
∴DG:EF=BD:BE,
∴BE=
| 3 |
在△ABE中,BE2=AB2+AE2-
| 1 |
| 2 |
即3(1-x)2=1+x2+x,
解得:x=
7+
| ||
| 4 |
7-
| ||
| 4 |
又由0<x<1,
∴x=
7-
| ||
| 4 |
即AE的最大值为
7-
| ||
| 4 |
点评:本题考查立体几何、平面几何、解析几何等基础知识,考查运算求解能力及应用意识,考查函数与方程思想、数形结合思想及化归与转化思想,本题考查的知识点是线面垂直的判定,空间两点之间距离,余弦定理,是解三角形与空间立体几何的综合应用,难度中档.

练习册系列答案
相关题目
在平面直角坐标系xOy中,已知
、
是互相垂直的两个单位向量,点Q满足
=3
+4
.曲线C={P|
=2
cosθ+2
sinθ,0≤θ≤2π},区域Ω={P|0<r≤|
|≤R,r<R}.若C∩Ω=C,则( )
| a |
| b |
| OQ |
| a |
| b |
| OP |
| a |
| b |
| PQ |
| A、0<r≤3且R≥7 |
| B、0<r≤3≤R≤7 |
| C、0<r≤5<R<7 |
| D、5≤r<7≤R |
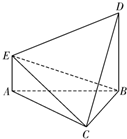 如图,在多面体ABCDE中,DB丄平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,AE=1,BD=2.
如图,在多面体ABCDE中,DB丄平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,AE=1,BD=2. 如图,在几何体ABCDE中,平面ABC⊥平面BCD,AE∥BD,△ABC为边长等于2的正三角形,CD=2
如图,在几何体ABCDE中,平面ABC⊥平面BCD,AE∥BD,△ABC为边长等于2的正三角形,CD=2