Question

设函数f（x）=|x-1|+|x-2|．
（Ⅰ）画出函数y=f（x）的图象；
（Ⅱ）若不等式|a+b|-|a-b|≤|a|•f（x）对任意a，b∈R且a≠0恒成立，求实数x的范围．

Answer 1

考点：绝对值不等式的解法,函数的图象

专题：选作题,不等式

分析：本题考查的是分段函数的解析式求法以及函数图象的作法问题．在解答时对（1）要先将原函数根据自变量的取值范围转化为分段函数，然后逐段画出图象；对（2）先结和条件a≠0将问题转化，见参数统统移到一边，结合绝对值不等式的性质找出f（x）的范围，通过图形即可解得结果．

解答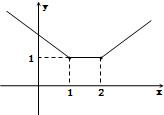： 解：（1）f（x）=

2x-3(x≥2) 1(1＜x＜2) 3-2x(x≤1)

，图象如图所示；
（2）由|a+b|-|a-b|≤|a|•f（x）得

|a+b|-|a-b|

|a|

≤f（x）
又因为

|a+b|-|a-b|

|a|

≤

|a+b+a-b|

|a|

=2
则有f（x）≥2
解不等式|x-1|+|x-2|≥2
得x≥

5

2

或x≤

1

2

，
∴实数x的范围是x≥

5

2

或x≤

1

2

．

点评：本题考查的是分段函数的解析式求法以及函数图象的作法问题．在解答过程中充分体现了分类讨论的思想、数形结合的思想、问题转化的思想．值得同学体会和反思．