题目内容
如图，四棱锥P-ABCD中，底面ABCD是菱形，∠ABC=60°侧面PAD⊥底面ABCD．E、F分别为AD、PA中点．
（1）求证：PD∥平面CEF；
（2）求证：平面CEF⊥平面PAD．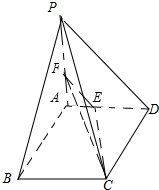
（1）求证：PD∥平面CEF；
（2）求证：平面CEF⊥平面PAD．
考点：平面与平面垂直的判定,直线与平面平行的判定
专题：证明题,空间位置关系与距离
分析：（1）利用E、F分别为AD、PA中点，可得EF∥PD，利用线面平行的判定定理，即可证明PD∥平面CEF；
（2）利用侧面PAD⊥底面ABCD，侧面PAD∩底面ABCD=AD，证明CE⊥侧面PAD，即可证明平面CEF⊥平面PAD．
（2）利用侧面PAD⊥底面ABCD，侧面PAD∩底面ABCD=AD，证明CE⊥侧面PAD，即可证明平面CEF⊥平面PAD．
解答：
证明：（1）∵E、F分别为AD、PA中点，
∴EF∥PD，
∵EF?平面CEF，PD?平面CEF，
∴PD∥平面CEF；
（2）由题意△ACD为正三角形，故CE⊥AD，
∵侧面PAD⊥底面ABCD，侧面PAD∩底面ABCD=AD，
∴CE⊥侧面PAD，
∵CE?平面CEF
∴平面CEF⊥平面PAD
∴EF∥PD，
∵EF?平面CEF，PD?平面CEF，
∴PD∥平面CEF；
（2）由题意△ACD为正三角形，故CE⊥AD，
∵侧面PAD⊥底面ABCD，侧面PAD∩底面ABCD=AD，
∴CE⊥侧面PAD，
∵CE?平面CEF
∴平面CEF⊥平面PAD
点评：本题考查直线与平面平行、平面与平面垂直的判定，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
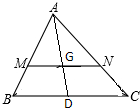如图，△ABC中，D为BC的中点，G为AD的中点，过点G任作一直线MN，分别交AB，AC于M，N两点，若
设函数f（x）=|x-1|+|x-2|．