题目内容
设函数f(x)=ex(sinx-cosx)(0≤x≤2011π),则函数f(x)的各极大值之和为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:利用导数研究函数的极值
专题:计算题,导数的综合应用
分析:由题意求导f′(x)=ex(sinx-cosx)+ex(cosx+sinx)=2exsinx=0;从而确定极值点,再确定极大值点,从而求极大值,再由等比数列求和.
解答:
解:∵f(x)=ex(sinx-cosx),
∴令f′(x)=ex(sinx-cosx)+ex(cosx+sinx)
=2exsinx=0;
则x=kπ,
故函数f(x)的极大值点为π+2kπ,
故函数f(x)的各极大值为eπ(sinπ-cosπ),e3π(sin3π-cos3π),e5π(sin5π-cos5π),…,e2009π(sin2009π-cos2009π);
即eπ,e3π,e5π,…,e2009π;
故其和为eπ+e3π+e5π+…+e2009π
=
=
;
故选D.
∴令f′(x)=ex(sinx-cosx)+ex(cosx+sinx)
=2exsinx=0;
则x=kπ,
故函数f(x)的极大值点为π+2kπ,
故函数f(x)的各极大值为eπ(sinπ-cosπ),e3π(sin3π-cos3π),e5π(sin5π-cos5π),…,e2009π(sin2009π-cos2009π);
即eπ,e3π,e5π,…,e2009π;
故其和为eπ+e3π+e5π+…+e2009π
=
| eπ(1-e2π•1005) |
| 1-e2π |
| eπ(1-e2010π) |
| 1-e2π |
故选D.
点评:本题考查了导数的综合应用,同时考查了三角函数及等比数列,属于中档题.

练习册系列答案
相关题目
 如图,分别以正方形ABCD的四条边为直径画半圆,重叠部分如图中阴影区域,若向该正方形内随机投一点,则该点落在空白区域的概率为( )
如图,分别以正方形ABCD的四条边为直径画半圆,重叠部分如图中阴影区域,若向该正方形内随机投一点,则该点落在空白区域的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
若原点O到直线ax+by+c=0的距离为1,则有( )
| A、c=1 | ||
B、c=
| ||
| C、c2=a2+b2 | ||
| D、c=a+b |
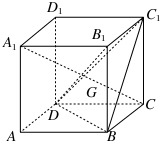 如图,在棱长为a的正方体ABCD-A1B1C1D1中,G为△BC1D的重心,
如图,在棱长为a的正方体ABCD-A1B1C1D1中,G为△BC1D的重心, 设函数f(x)=|x-1|+|x-2|.
设函数f(x)=|x-1|+|x-2|.