题目内容
已知x,y满足方程x2+y2-4x+1=0,则y-x的最大值为 ;x2+y2最小值为 .
考点:直线和圆的方程的应用
专题:综合题,直线与圆
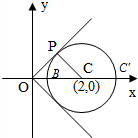
分析:设y-x=b,仅当直线y=x+b与圆切于第四象限时,纵轴截距b取最小值.进而利用点到直线的距离求得y-x的最小值;x2+y2是圆上点与原点距离之平方,故连接OC,与圆交于B点,并延长交圆于C′,进而可知x2+y2的最大值和最小值分别为|OC′|和|OB|,答案可得.
解答:
解:方程x2+y2-4x+1=0表示以点(2,0)为圆心,以
为半径的圆
设y-x=b,则y=x+b,仅当直线y=x+b与圆切于第四象限时,纵轴截距b取最小值.
由点到直线的距离公式,得
=
,即b=-2±
,
故(y-x)min=-2-
.
(3)x2+y2是圆上点与原点距离之平方,故连接OC,与圆交于B点,并延长交圆于C′,可知B到原点的距离最近,点C′到原点的距离最大,此时有OB=2-
,
∴(x2+y2)min=|OB|2=7-4
.
故答案为:-2-
;7-4
.
| 3 |
设y-x=b,则y=x+b,仅当直线y=x+b与圆切于第四象限时,纵轴截距b取最小值.
由点到直线的距离公式,得
| |2-0+b| | ||
|
| 3 |
| 6 |

故(y-x)min=-2-
| 6 |
(3)x2+y2是圆上点与原点距离之平方,故连接OC,与圆交于B点,并延长交圆于C′,可知B到原点的距离最近,点C′到原点的距离最大,此时有OB=2-
| 3 |
∴(x2+y2)min=|OB|2=7-4
| 3 |
故答案为:-2-
| 6 |
| 3 |
点评:本题主要考查了圆的方程的综合运用.考查了学生转化和化归的思想和数形结合的思想.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
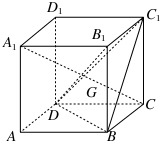 如图,在棱长为a的正方体ABCD-A1B1C1D1中,G为△BC1D的重心,
如图,在棱长为a的正方体ABCD-A1B1C1D1中,G为△BC1D的重心, 设函数f(x)=|x-1|+|x-2|.
设函数f(x)=|x-1|+|x-2|.