��Ŀ����
��ͼչʾ��һ�����䣨0��k����k��һ����������ʵ������ʵ����R�Ķ�Ӧ���̣����䣨0��k���е�ʵ��m��Ӧ�߶�AB�ϵĵ�M����ͼ1�����߶�AB��ɰ�Բ����Բ��ΪH����ͼ2���ٽ������Բ����ֱ������ϵ�У�ʹ��Բ��H����Ϊ��0��1����ֱ��ABƽ��x�ᣬ��ͼ3����ͼ�α仯�����У�ͼ1���߶�AM�ij��ȶ�Ӧ��ͼ3�е�Բ��AM�ij��ȣ�ֱ��HM��ֱ��y=-1�ཻ���N��n��-1��������ʵ��m��Ӧ��ʵ������n������n=f��m���������������⣺
��1��f��
��=6��
��2������n=f��m�����溯����
��3��n=f��m���Ƕ������ϵĵ�������������
��4��n=f��m����ͼ����ڵ㣨
��0���Գƣ�
��5������f��m��=2�Ľ���m=
k��
������ȷ�������Ϊ ��

��1��f��
| k |
| 4 |
��2������n=f��m�����溯����
��3��n=f��m���Ƕ������ϵĵ�������������
��4��n=f��m����ͼ����ڵ㣨
| k |
| 2 |
��5������f��m��=2�Ľ���m=
| 3 |
| 4 |
������ȷ�������Ϊ

���㣺����ʵ������ѡ��������
ר�⣺������,���������ʼ�Ӧ��
�����������⣬������ȷ��Ӧ��ϵ��m���Ӧ��MH����б�ǵı䣬�Ӷ����n���Ӷ������������жϣ�
���
�⣺��1����m=
ʱ����AM=
��AB��
�ʿ�֪HM����б��Ϊ45�㣻
��ֱ��HM�ķ���Ϊy=x+1��
��y=-1�ã�x=-2��
��f��
��=2���ʲ���ȷ��
��2������n=f��m���Ķ�����Ϊ��0��k�����ʲ��������溯�����ʲ���ȷ��
��3��������֪����m���ʱ��ֱ��HM��y=-1�Ľ��������ƶ���
��nҲ�ڱ��n=f��m���Ƕ������ϵĵ�����������������ȷ��
��4����m=
ʱ����֪n=0��
��m��
ʱ��ֱ��HM����б�Ǧ�=
����
��ֱ��HM�ķ���Ϊy=xtan
��+1��
��y=-1�ã�x=-
��
��n=-
�����㣨m��-
����n=f��m����ͼ���ϣ�
m����
�ԳƵ�����k-m����ʱֱ��HM����б��Ϊ��-
����
ֱ��HM�ķ���Ϊy=xtan����-
����+1=-xtan
��+1��
��y=-1�ã�x=
��
��n=
��
�ʵ㣨k-m��
����n=f��m����ͼ���ϣ�
��n=f��m����ͼ����ڵ㣨
��0���Գƣ�����ȷ��
��5����f��m��=2�ã�ֱ��HM���㣨0��1������2��-1����
��ֱ��HM��б��Ϊ-1��
��ֱ��HM����б��Ϊ
����
��
��=
������m=
k��
����ȷ��
�ʴ�Ϊ����3������4������5����
| k |
| 4 |
| 1 |
| 4 |
�ʿ�֪HM����б��Ϊ45�㣻
��ֱ��HM�ķ���Ϊy=x+1��
��y=-1�ã�x=-2��
��f��
| k |
| 4 |
��2������n=f��m���Ķ�����Ϊ��0��k�����ʲ��������溯�����ʲ���ȷ��
��3��������֪����m���ʱ��ֱ��HM��y=-1�Ľ��������ƶ���
��nҲ�ڱ��n=f��m���Ƕ������ϵĵ�����������������ȷ��
��4����m=
| k |
| 2 |
��m��
| k |
| 2 |
| m |
| k |
��ֱ��HM�ķ���Ϊy=xtan
| m |
| k |
��y=-1�ã�x=-
| 2 | ||
tan
|
��n=-
| 2 | ||
tan
|
| 2 | ||
tan
|
m����
| k |
| 2 |
| m |
| k |
ֱ��HM�ķ���Ϊy=xtan����-
| m |
| k |
| m |
| k |
��y=-1�ã�x=
| 2 | ||
tan
|
��n=
| 2 | ||
tan
|
�ʵ㣨k-m��
| 2 | ||
tan
|
��n=f��m����ͼ����ڵ㣨
| k |
| 2 |
��5����f��m��=2�ã�ֱ��HM���㣨0��1������2��-1����
��ֱ��HM��б��Ϊ-1��
��ֱ��HM����б��Ϊ
| 3 |
| 4 |
��
| m |
| k |
| 3 |
| 4 |
| 3 |
| 4 |
����ȷ��
�ʴ�Ϊ����3������4������5����
���������⿼����ѧ�������¶���Ľ���������ͬʱ������ӳ��ı���Ӧ�ã��������⣮

��ϰ��ϵ�д�
�����Ŀ
��Ǹ�ʵ��x��y����x-y+1��0��3x+y-3��0����4x+y�����ֵΪ��������
| A��1 | ||
B��
| ||
C��
| ||
| D��4 |
 ��ͼ���ֱ���������ABCD��������Ϊֱ������Բ���ص�������ͼ����Ӱ��������������������Ͷһ�㣬��õ����ڿհ�����ĸ���Ϊ��������
��ͼ���ֱ���������ABCD��������Ϊֱ������Բ���ص�������ͼ����Ӱ��������������������Ͷһ�㣬��õ����ڿհ�����ĸ���Ϊ��������A��
| ||
B��
| ||
C��
| ||
D��
|
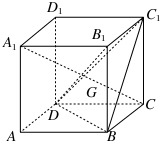 ��ͼ�����ⳤΪa��������ABCD-A1B1C1D1�У�GΪ��BC1D�����ģ�
��ͼ�����ⳤΪa��������ABCD-A1B1C1D1�У�GΪ��BC1D�����ģ� �躯��f��x��=|x-1|+|x-2|��
�躯��f��x��=|x-1|+|x-2|��