题目内容
 在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,D是AB中点,(直三棱柱,指侧棱垂直于底面的棱柱).
在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,D是AB中点,(直三棱柱,指侧棱垂直于底面的棱柱).(1)求证:AC⊥BC1;
(2)求证:AC1∥平面CDB1
(3)求点C到平面ABC1的距离.
考点:点、线、面间的距离计算,直线与平面平行的判定
专题:综合题,空间位置关系与距离
分析:(1)利用勾股定理的逆定理判断出AC⊥BC,同时因为三棱柱为直三棱柱,从而证出.
(2)因为D为AB的中点,连接C1B和CB1交点为E,连接DE,∵D是AB的中点,E是BC1的中点,根据三角形中位线定理得DE∥AC1,得到AC1∥平面CDB1;
(3)利用等体积,求点C到平面ABC1的距离.
(2)因为D为AB的中点,连接C1B和CB1交点为E,连接DE,∵D是AB的中点,E是BC1的中点,根据三角形中位线定理得DE∥AC1,得到AC1∥平面CDB1;
(3)利用等体积,求点C到平面ABC1的距离.
解答:
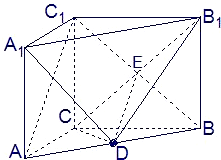 (1)证明:直三棱柱ABC-A1B1C1,底面三边长AC=3,BC=4,AB=5,
(1)证明:直三棱柱ABC-A1B1C1,底面三边长AC=3,BC=4,AB=5,
∴AC⊥BC,且BC1在平面ABC内的射影为BC,∴AC⊥BC1;
(2)证明:设CB1与C1B的交点为E,连接DE,
∵D是AB的中点,E是BC1的中点,
∴DE∥AC1,
∵DE?平面CDB1,AC1?平面CDB1,
∴AC1∥平面CDB1;
(3)解:△ABC1中,AB=5,AC1=5,BC1=4
,
∴S△ABC1=
×4
×
=2
,
设点C到平面ABC1的距离为h,则
×2
h=
×
×3×4×4=
,
∴点C到平面ABC1的距离为
.
 (1)证明:直三棱柱ABC-A1B1C1,底面三边长AC=3,BC=4,AB=5,
(1)证明:直三棱柱ABC-A1B1C1,底面三边长AC=3,BC=4,AB=5,∴AC⊥BC,且BC1在平面ABC内的射影为BC,∴AC⊥BC1;
(2)证明:设CB1与C1B的交点为E,连接DE,
∵D是AB的中点,E是BC1的中点,
∴DE∥AC1,
∵DE?平面CDB1,AC1?平面CDB1,
∴AC1∥平面CDB1;
(3)解:△ABC1中,AB=5,AC1=5,BC1=4
| 2 |
∴S△ABC1=
| 1 |
| 2 |
| 2 |
| 25-8 |
| 34 |
设点C到平面ABC1的距离为h,则
| 1 |
| 3 |
| 34 |
| 1 |
| 3 |
| 1 |
| 2 |
| 6 |
| 17 |
| 34 |
∴点C到平面ABC1的距离为
| 6 |
| 17 |
| 34 |
点评:本题考查线面垂直,考查线面平行,考查等体积,求点C到平面ABC1的距离,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
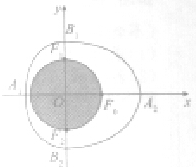 某服饰公司设计类一款服饰饰品,如图外面是红色透明水晶材质,里面是一个球形绿色玉质宝珠,其轴截面呦半椭圆C1:
某服饰公司设计类一款服饰饰品,如图外面是红色透明水晶材质,里面是一个球形绿色玉质宝珠,其轴截面呦半椭圆C1: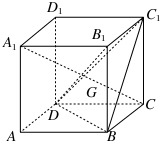 如图,在棱长为a的正方体ABCD-A1B1C1D1中,G为△BC1D的重心,
如图,在棱长为a的正方体ABCD-A1B1C1D1中,G为△BC1D的重心,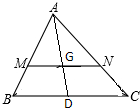 如图,△ABC中,D为BC的中点,G为AD的中点,过点G任作一直线MN,分别交AB,AC于M,N两点,若
如图,△ABC中,D为BC的中点,G为AD的中点,过点G任作一直线MN,分别交AB,AC于M,N两点,若 设函数f(x)=|x-1|+|x-2|.
设函数f(x)=|x-1|+|x-2|.