题目内容
在锐角△ABC中,角A,B,C的对边分别为a,b,c.已知sin(A-B)=cosC.
(Ⅰ)若a=3
,b=
,求c;
(Ⅱ)求
的取值范围.
(Ⅰ)若a=3
| 2 |
| 10 |
(Ⅱ)求
| acosC-ccosA |
| b |
考点:余弦定理,正弦定理
专题:三角函数的求值
分析:(Ⅰ)已知等式右边利用诱导公式化简,根据三角形ABC为锐角三角形确定出B的度数,再由a与b的值,利用余弦定理即可求出c;
(Ⅱ)由B的度数求出A+C的度数,用A表示出C,代入所求式子,利用两角和与差的正弦函数公式及正弦定理化简,根据正弦函数的值域即可确定出范围.
(Ⅱ)由B的度数求出A+C的度数,用A表示出C,代入所求式子,利用两角和与差的正弦函数公式及正弦定理化简,根据正弦函数的值域即可确定出范围.
解答:
解:(Ⅰ)由sin(A-B)=cosC,得sin(A-B)=sin(
-C),
∵△ABC是锐角三角形,
∴A-B=
-C,即A-B+C=
,①
又A+B+C=π,②
由②-①,得B=
,
由余弦定理b2=c2+a2-2cacosB,得(
)2=c2+(3
)2-2c×3
cos
,
整理得:c2-6c+8=0,
解得:c=2,或c=4,
当c=2时,b2+c2-a2=(
)2+22-(3
)2=-4<0,
∴b2+c2<a2,此时A为钝角,与已知矛盾,故c≠2,
则c=4;
(Ⅱ)由(Ⅰ),知B=
,
∴A+C=
,即C=
-A,
∴利用正弦定理化简得:
=
=
=
sin(2A-
),
∵△ABC是锐角三角形,
∴
<A<
,
∴-
<2A-
<
,
∴-
<sin(2A-
)<
,
∴-1<
<1.
则
的取值范围为(-1,1).
| π |
| 2 |
∵△ABC是锐角三角形,
∴A-B=
| π |
| 2 |
| π |
| 2 |
又A+B+C=π,②
由②-①,得B=
| π |
| 4 |
由余弦定理b2=c2+a2-2cacosB,得(
| 10 |
| 2 |
| 2 |
| π |
| 4 |
整理得:c2-6c+8=0,
解得:c=2,或c=4,
当c=2时,b2+c2-a2=(
| 10 |
| 2 |
∴b2+c2<a2,此时A为钝角,与已知矛盾,故c≠2,
则c=4;
(Ⅱ)由(Ⅰ),知B=
| π |
| 4 |
∴A+C=
| 3π |
| 4 |
| 3π |
| 4 |
∴利用正弦定理化简得:
| acosC-ccosA |
| b |
| sinAcosC-cosAsinC |
| sinB |
| sin(A-C) | ||||
|
| 2 |
| 3π |
| 4 |
∵△ABC是锐角三角形,
∴
| π |
| 4 |
| π |
| 2 |
∴-
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
∴-
| ||
| 2 |
| 3π |
| 4 |
| ||
| 2 |
∴-1<
| acosC-ccosA |
| b |
则
| acosC-ccosA |
| b |
点评:此题考查了正弦、余弦定理,以及正弦函数的值域,熟练掌握定理是解本题的关键.

练习册系列答案
相关题目
若f(x)=3x5+4x4+5x3+2x2+2x+1,当x=2时,则V4的值为( )
| A、50 | B、52 |
| C、104 | D、106 |
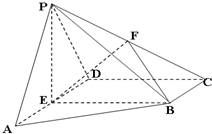 已知在四棱锥P-ABCD中,AD∥BC,AD⊥CD,PA=PD=AD=2BC=2CD,E,F分别是AD,PC的中点.
已知在四棱锥P-ABCD中,AD∥BC,AD⊥CD,PA=PD=AD=2BC=2CD,E,F分别是AD,PC的中点.