题目内容
已知数列{an}中,a1=6,an+1+an=3•2n+1,n∈N*.
(Ⅰ)设bn=an-2n+1,证明:数列{bn}是等比数列;
(Ⅱ)在数列{an}中,是否存在连续三项成等差数列?若存在,求出所有符合条件的项;若不存在,请说明理由;
(Ⅲ)若1<r<s且r,s∈N*,求证:使得a1,ar,as成等差数列的点列(r,s)在某一条直线上.
(Ⅰ)设bn=an-2n+1,证明:数列{bn}是等比数列;
(Ⅱ)在数列{an}中,是否存在连续三项成等差数列?若存在,求出所有符合条件的项;若不存在,请说明理由;
(Ⅲ)若1<r<s且r,s∈N*,求证:使得a1,ar,as成等差数列的点列(r,s)在某一条直线上.
考点:等比数列的性质,等差数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)将条件变形,构造符合条件的数列,即可证明数列{an-2n}是等比数列,从而可求数列{an}的通项公式;
(Ⅱ)假设在数列{an}中存在连续三项成等差数列,代入相应的项,化简可得结论;
(Ⅲ)若a1,ar,as成等差数列,则2ar=a1+as,代入变形整理,对r、s进行讨论,可得结论.
(Ⅱ)假设在数列{an}中存在连续三项成等差数列,代入相应的项,化简可得结论;
(Ⅲ)若a1,ar,as成等差数列,则2ar=a1+as,代入变形整理,对r、s进行讨论,可得结论.
解答:
(Ⅰ)证明:∵an+1+an=3•2n+1,
∴an+1-2n+2=-an+3•2n+1-2n+2,
化简可得an+1-2n+2=-(an-2n+1),
即bn+1=-bn,
又a1=6,
∴b1=a1-22=6-4=2≠0,
∴数列{bn}是等比数列;
(Ⅱ)解:由(Ⅰ)知b1=a1-21+1=2,公比q=-1,
得bn=2×(-1)n-1,
又bn=an-2n+1,
∴an=2n+1+2×(-1)n-1.
假设在数列{an}中存在连续三项ak,ak+1,ak+2成等差数列,
则有2×(2k+1+1+2×(-1)k+1-1)=2k+1+2×(-1)k-1+2k+2+12×(-1)k+2-1,
化简可得(-1)k=2k-1+(-1)k+1,
当k取偶数2时,上式成立,
故存在满足条件的连续三项a2,a3,a4为成等差数列;
(Ⅲ)证明:若1<r<s且r,s∈N*,
要使得a1,ar,as成等差数列,
则2ar=a1+as,
即2[2×(-1)r-1+2r+1]=6+2×(-1)s-1+2s+1,
变形得:2(-1)r-1+2•2r=3+(-1)s-1+2s,
由于r,s∈N*且1<r<s,下面对r、s进行讨论:
①若r,s均为偶数,则2s-2r+1=-4<0,解得s<r+1,与1<r<s矛盾,舍去;
②若r为奇数,s为偶数,则2s-2r+1=0,解得s=r+1;
③若r为偶数,s为奇数,则2s-2r+1<0,解得s<r+1,与1<r<s矛盾,舍去;
④若r,s均为奇数,则2s-2r+1<0,解得s<r+1,与1<r<s矛盾,舍去;
综上①②③④可知,只有当r为奇数,s为偶数时,a1,ar,as成等差数列,
此时满足条件点列(r,s)落在直线y=x+1(其中为正奇数)上.
∴点列(r,s)在某一条直线上.
∴an+1-2n+2=-an+3•2n+1-2n+2,
化简可得an+1-2n+2=-(an-2n+1),
即bn+1=-bn,
又a1=6,
∴b1=a1-22=6-4=2≠0,
∴数列{bn}是等比数列;
(Ⅱ)解:由(Ⅰ)知b1=a1-21+1=2,公比q=-1,
得bn=2×(-1)n-1,
又bn=an-2n+1,
∴an=2n+1+2×(-1)n-1.
假设在数列{an}中存在连续三项ak,ak+1,ak+2成等差数列,
则有2×(2k+1+1+2×(-1)k+1-1)=2k+1+2×(-1)k-1+2k+2+12×(-1)k+2-1,
化简可得(-1)k=2k-1+(-1)k+1,
当k取偶数2时,上式成立,
故存在满足条件的连续三项a2,a3,a4为成等差数列;
(Ⅲ)证明:若1<r<s且r,s∈N*,
要使得a1,ar,as成等差数列,
则2ar=a1+as,
即2[2×(-1)r-1+2r+1]=6+2×(-1)s-1+2s+1,
变形得:2(-1)r-1+2•2r=3+(-1)s-1+2s,
由于r,s∈N*且1<r<s,下面对r、s进行讨论:
①若r,s均为偶数,则2s-2r+1=-4<0,解得s<r+1,与1<r<s矛盾,舍去;
②若r为奇数,s为偶数,则2s-2r+1=0,解得s=r+1;
③若r为偶数,s为奇数,则2s-2r+1<0,解得s<r+1,与1<r<s矛盾,舍去;
④若r,s均为奇数,则2s-2r+1<0,解得s<r+1,与1<r<s矛盾,舍去;
综上①②③④可知,只有当r为奇数,s为偶数时,a1,ar,as成等差数列,
此时满足条件点列(r,s)落在直线y=x+1(其中为正奇数)上.
∴点列(r,s)在某一条直线上.
点评:本题考查数列递推式,考查等比数列的证明,考查数列的通项,考查分类讨论的数学思想,考查学生分析解决问题的能力,有难度.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
1426和1643的最大公约数是( )
| A、34 | B、12 | C、93 | D、31 |
已知α是第四象限的角,且sinα•cosα=-
,则sinα-cosα=( )
| 12 |
| 25 |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
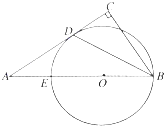 如图,在Rt△ABC中,∠C=90°,E为AB上一点,以BE为直径作圆O与AC相切于点D.若AB:BC=2:1,CD=
如图,在Rt△ABC中,∠C=90°,E为AB上一点,以BE为直径作圆O与AC相切于点D.若AB:BC=2:1,CD=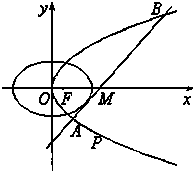 已知椭圆C1和抛物线C2有公共焦点F(1,0),C1的中心和C2的顶点都在坐标原点,过点M(4,0)的直线l与抛物线C2分别相交于A,B两点.
已知椭圆C1和抛物线C2有公共焦点F(1,0),C1的中心和C2的顶点都在坐标原点,过点M(4,0)的直线l与抛物线C2分别相交于A,B两点.