题目内容
4.函数f(x)=ln|x|+|sinx|(-π≤x≤π且x≠0)的图象大致是( )| A. |  | B. | 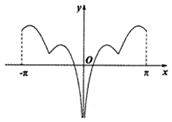 | ||
| C. |  | D. |  |
分析 利用函数的奇偶性排除选项,通过函数的导数求解函数的极值点的个数,求出f(π)的值,推出结果即可.
解答  解:函数f(x)=ln|x|+|sinx|(-π≤x≤π且x≠0)是偶函数排除A.
解:函数f(x)=ln|x|+|sinx|(-π≤x≤π且x≠0)是偶函数排除A.
当x>0时,f(x)=lnx+sinx,可得:f′(x)=$\frac{1}{x}$+cosx,令$\frac{1}{x}$+cosx=0,
作出y=$\frac{1}{x}$与y=-cosx图象如图:可知两个函数有一个交点,就是函数有一个极值点.
f(π)=lnπ>1,
故选:D.
点评 本题考查函数的奇偶性以及函数的导数的应用,函数的极值,考查转化思想以及计算能力.

练习册系列答案
相关题目
14.已知集合A={x∈Z|-1≤x≤2},B={x|log3x<1},则A∩B=( )
| A. | {-1,0,1,2} | B. | {0,1,2} | C. | {0,1} | D. | {1,2} |
15.下列结论中正确的是( )
| A. | ∵a∥α,b∥α,∴a∥b | B. | ∵a∥α,b?α,∴a∥b | C. | ∵α∥β,a∥β,∴a∥α | D. | ∵α∥β,a?β,∴a∥α |
16.在△ABC中,角A,B,C所对的边分别为a,b,c,若1+$\frac{tanA}{tanB}$=$\frac{2c}{b}$,则A=( )
| A. | 30°? | B. | 45°? | C. | 60°? | D. | 120°? |